Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Một mặt phẳng (P) đồng thời song song với AC và SB lần lượt cắt các đoạn thẳng SA, AB, BC, SC, SD và BD tại M, N, E, F, I, J. Xét các khẳng định sau:
(1) MN // (SCD) (2) EF // (SAD)
(3) NE // (SAC) (3) IJ // (SAB)
Có bao nhiêu khẳng định đúng?
Phương pháp giải
- Đưa về cùng mặt phẳng
- Chứng minh đường thẳng song song với mặt phẳng a // b \( \subset \left( P \right) \Rightarrow \)a // (P).
Lời giải của Tự Học 365
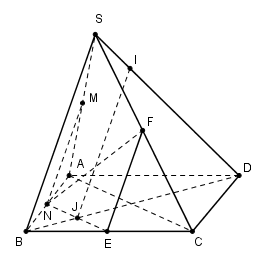
Trước hết ta lấy điểm \(M \in \left( P \right)\) sao cho \(M \in SA\).
Trong mp(SAB) kẻ MN // SA \(\left( {N \in AB} \right)\), trong mp(ABCD) kẻ NE // AC \(\left( {E \in BC} \right)\).
\(NE \cap BD = \left\{ J \right\}\)
Trong mp(SBC) kẻ EF // SB \(\left( {F \in SC} \right)\), trong mp(SBD) kẻ JI // SD \(\left( {I \in SD} \right)\).
Giả sử MN // (SCD)
Lại có: MN // SB\( \Rightarrow SB \subset \left( {SCD} \right)\) (vô lý) nên (1) sai.
Tương tự ta chứng minh được (2) sai.
NE // AC\( \subset \left( {SAC} \right) \Rightarrow \) NE // (SAC). Do đó (3) đúng.
IJ // SB\( \subset \left( {SAB} \right) \Rightarrow \)IJ // (SAB). Do đó (4) đúng.
Đáp án cần chọn là: b
Toán Lớp 12
