Câu hỏi
Thông hiểu
Tam thức bậc hai $f\left( x \right) = {x^2} + \left( {\sqrt 5 - 1} \right)x - \sqrt 5 $ nhận giá trị dương khi và chỉ khi
Đáp án đúng: c
Phương pháp giải
Tìm các nghiệm của \(f\left( x \right)\), lập bảng xét dấu và kết luận.
Lời giải của Tự Học 365
Ta có $f\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - \sqrt 5 \end{array} \right.$.
Bảng xét dấu:
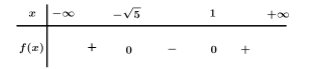
Dựa vào bảng xét dấu $f\left( x \right) > 0 \Leftrightarrow x \in \left( { - \infty ; - \sqrt 5 } \right) \cup \left( {1; + \infty } \right).$
Đáp án cần chọn là: c
Toán Lớp 12
