Lời giải của Tự Học 365

Đặt $f\left( x \right) = \left( {2 - x} \right)\left( {x + 1} \right)\left( {3 - x} \right)$

Phương trình $2 - x = 0 \Leftrightarrow x = 2;\,\,\,x + 1 = 0 \Leftrightarrow x =  - \,1$ và $3 - x = 0 \Leftrightarrow x = 3.$

Ta có bảng xét dấu

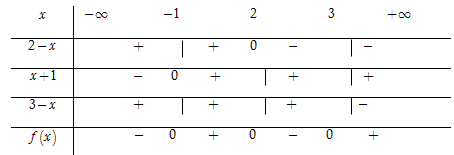
Dựa vào bảng xét dấu, ta thấy rằng $f\left( x \right) \le 0 \Leftrightarrow x \in \left( { - \,\infty ; - \,1} \right] \cup \left[ {2;3} \right].$

Vậy bất phương trình đã cho có $2$ nghiệm nguyên dương.

Đáp án cần chọn là: d