Lời giải của Tự Học 365

Xét bất phương trình $\left| {x + 2} \right| - \left| {x - 1} \right| \le x - \dfrac{3}{2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left(  *  \right).$

Lập bảng xét dấu

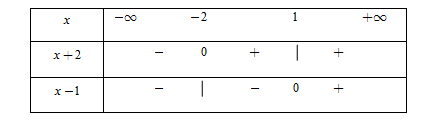
TH1. Với $x <  - \,2,$ khi đó $\left(  *  \right) \Leftrightarrow  - \,x - 2 + x - 1 < x - \dfrac{3}{2} \Leftrightarrow x >  - \dfrac{3}{2}.$

Kết hợp với điều kiện $x <  - \,2,$ ta được tập nghiệm ${S_1} = \emptyset .$

TH2. Với $ - \,2 \le x < 1,$ khi đó $\left(  *  \right) \Leftrightarrow x + 2 + x - 1 < x - \dfrac{3}{2} \Leftrightarrow x <  - \dfrac{5}{2}.$

Kết hợp với điều kiện $ - \,2 \le x < 1,$ ta được tập nghiệm ${S_2} = \emptyset .$

TH3. Với $x \ge 1,$ khi đó $\left(  *  \right) \Leftrightarrow x + 2 - x + 1 < x - \dfrac{3}{2} \Leftrightarrow x > \dfrac{9}{2}.$

Kết hợp với điều kiện $x \ge 1,$ ta được tập nghiệm ${S_3} = \left( {\dfrac{9}{2}; + \,\infty } \right).$

Vậy tập nghiệm của bất phương trình là $S = {S_1} \cup {S_2} \cup {S_3} = \left( {\dfrac{9}{2}; + \,\infty } \right).$

Đáp án cần chọn là: d