Lời giải của Tự Học 365

Bất phương trình $\dfrac{1}{{x + 1}} < \dfrac{1}{{{{\left( {x - 1} \right)}^2}}} \Leftrightarrow \dfrac{1}{{x + 1}} - \dfrac{1}{{{{\left( {x - 1} \right)}^2}}} < 0.$

$ \Leftrightarrow \dfrac{{{{\left( {x - 1} \right)}^2} - \left( {x + 1} \right)}}{{\left( {x + 1} \right){{\left( {x - 1} \right)}^2}}} < 0 \Leftrightarrow \dfrac{{x\left( {x - 3} \right)}}{{\left( {x + 1} \right){{\left( {x - 1} \right)}^2}}} < 0 \Leftrightarrow \left\{ \begin{array}{l}x e 1\\\dfrac{{x\left( {x - 3} \right)}}{{x + 1}} < 0\end{array} \right.$ (vì ${\left( {x - 1} \right)^2} > 0,\,\,\forall x e 1$).

Đặt $f\left( x \right) = \dfrac{{x\left( {x - 3} \right)}}{{x + 1}}.$ Ta có $x - 3 = 0 \Leftrightarrow x = 3$ và $x + 1 = 0 \Leftrightarrow x =  - \,1.$

Bảng xét dấu

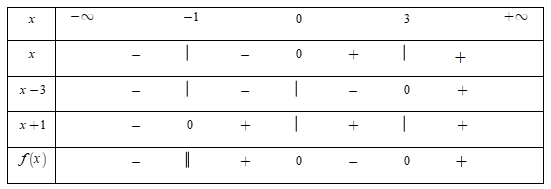
Dựa vào bảng xét dấu, ta thấy rằng $f\left( x \right) < 0 \Leftrightarrow \left[ \begin{array}{l}x <  - \,1\\0 < x < 3\end{array} \right..$

Kết hợp với điều kiện $x e 1,$ ta được tập nghiệm $S = \left( { - \,\infty ; - \,1} \right) \cup \left( {0;1} \right) \cup \left( {1;3} \right).$

Đáp án cần chọn là: c