Lời giải của Tự Học 365

Bất phương trình $\left( {3x - 6} \right)\left( {x - 2} \right)\left( {x + 2} \right)\left( {x - 1} \right) > 0 \Leftrightarrow 3{\left( {x - 2} \right)^2}\left( {x + 2} \right)\left( {x - 1} \right) > 0$

Vì ${\left( {x - 2} \right)^2} > 0,\,\,\forall x e 2$ nên bất phương trình trở thành $\left\{ \begin{array}{l}x e 2\\\left( {x + 2} \right)\left( {x - 1} \right) > 0\end{array} \right..$

Đặt $f\left( x \right) = \left( {x + 2} \right)\left( {x - 1} \right).$

Phương trình $x + 2 = 0 \Leftrightarrow x =  - \,2$ và $x - 1 = 0 \Leftrightarrow x = 1.$

Ta có bảng xét dấu

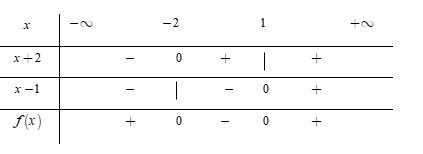
Dựa vào bảng xét dấu, ta thấy rằng $f\left( x \right) > 0$$ \Leftrightarrow x \in \left( { - \,\infty ; - \,2} \right) \cup \left( {1; + \,\infty } \right).$

Kết hợp với điều kiện $x e 2,$ ta được $ \Leftrightarrow x \in \left( { - \,\infty ; - \,2} \right) \cup \left( {1;2} \right) \cup \left( {2; + \,\infty } \right).$

Do đó, nghiệm nguyên âm lớn nhất của bất phương trình là $ - \,3$ và nghiệm nguyên dương nhỏ nhất của bất phương trình là $3.$

Vậy tích cần tính là $\left( { - \,3} \right).3 =  - \,9.$

Đáp án cần chọn là: a