Cho biểu thức \(f\left( x \right) = \dfrac{{2 - x}}{{x + 1}} + 2.\) Tập hợp tất cả các giá trị của \(x\) thỏa mãn bất phương trình \(f\left( x \right) < 0\) là
Phương pháp giải
- Rút gọn \(f\left( x \right)\) đưa \(f\left( x \right)\) về dạng thương của các nhị thức bậc nhất.
- Xét dấu các nhị thức bậc nhất đó rồi suy ra dấu của \(f\left( x \right)\).
Lời giải của Tự Học 365
- Ta có $f\left( x \right) = \dfrac{{2 - x}}{{x + 1}} + 2 = \dfrac{{2 - x + 2\left( {x + 1} \right)}}{{x + 1}} = \dfrac{{x + 4}}{{x + 1}}.$
Phương trình $x + 4 = 0 \Leftrightarrow x = - \,4$ và $x + 1 = 0 \Leftrightarrow x = - \,1.$
- Bảng xét dấu
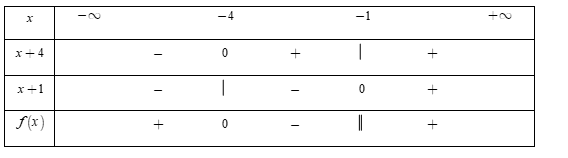
Dựa vào bảng xét dấu, ta thấy rằng $f\left( x \right) < 0 \Leftrightarrow x \in \left( { - \,4; - \,1} \right).$
Đáp án cần chọn là: c
Toán Lớp 12
