Lời giải của Tự Học 365

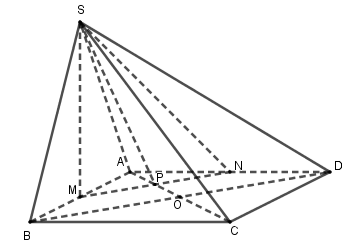
\( \bullet \) \(S\) là điểm chung thứ nhất giữa hai mặt phẳng \(\left( {SMN} \right)\) và \(\left( {SAC} \right).\)

\( \bullet \)  Trong mặt phẳng \(\left( {ABCD} \right)\), gọi \(P = MN \cap AC\).

\( \Rightarrow \left\{ \begin{array}{l}P \in AC \subset \left( {SAC} \right) \Rightarrow P \in \left( {SAC} \right)\\P \in MN \subset \left( {SMN} \right) \Rightarrow P \in \left( {SMN} \right)\end{array} \right.\) \( \Rightarrow P\) là điểm chung thứ hai giữa hai mặt phẳng \(\left( {SMN} \right)\) và \(\left( {SAC} \right).\)

Vậy \(\left( {SMN} \right) \cap \left( {SAC} \right) = SP\).

Gọi \(O\) là tâm hình bình hành ta có: \(\dfrac{{AP}}{{AC}} = \dfrac{1}{2}.\dfrac{{AP}}{{AO}} = \dfrac{1}{2}.\dfrac{{AM}}{{AB}} = \dfrac{1}{2}.\dfrac{1}{2} = \dfrac{1}{4}\) \( \Rightarrow AP = \dfrac{1}{4}AC \Rightarrow \overrightarrow {AP}  = \dfrac{1}{4}\overrightarrow {AC} \).

Đáp án cần chọn là: c