Cho tứ diện \(ABCD\), gọi \(M,N\) lần lượt là hai điểm thuộc các đoạn thẳng \(AB,AC\). Giao tuyến của hai mặt phẳng \(\left( {DBN} \right)\) và \(\left( {DCM} \right)\) là
Phương pháp giải
- Dựng hình, xác định điểm chung thứ nhất của hai mặt phẳng.
- Tìm điểm chung thứ hai (tìm hai đường thẳng lần lượt thuộc hai mặt phẳng mà cắt nhau).
Lời giải của Tự Học 365
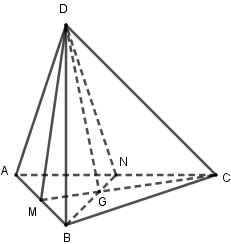
Dễ thấy \(D\) là điểm chung thứ nhất của hai mặt phẳng.
Trong mp\(\left( {ABC} \right)\) gọi \(G = BN \cap CM\) \( \Rightarrow \left\{ \begin{array}{l}G \in BN \subset \left( {BDN} \right)\\G \in CM \subset \left( {DCM} \right)\end{array} \right.\) \( \Rightarrow G \in \left( {DBN} \right) \cap \left( {DCM} \right)\)
\( \Rightarrow DG = \left( {DBN} \right) \cap \left( {DCM} \right)\).
Do \(M,N\) là các điểm bát kì thuộc hai đoạn thẳng \(AB,AC\) nên ta chưa thể kết luận được vị trí của \(G\).
Đáp án cần chọn là: b
Toán Lớp 12
