Lời giải của Tự Học 365

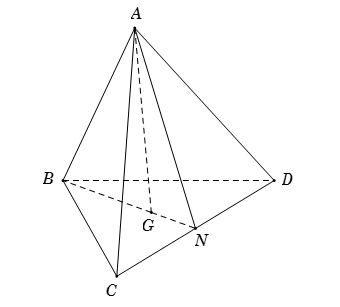
\( \bullet \) \(A\) là điểm chung thứ nhất giữa hai mặt phẳng \(\left( {ACD} \right)\) và \(\left( {GAB} \right).\)

\( \bullet \) Ta có \(BG \cap CD = N\) \( \Rightarrow \left\{ \begin{array}{l}N \in BG \subset \left( {ABG} \right) \Rightarrow N \in \left( {ABG} \right)\\N \in CD \subset \left( {ACD} \right) \Rightarrow N \in \left( {ACD} \right)\end{array} \right.\)

\( \Rightarrow N\)  là điểm chung thứ hai giữa hai mặt phẳng \(\left( {ACD} \right)\) và \(\left( {GAB} \right).\)

Vậy \(\left( {ABG} \right) \cap \left( {ACD} \right) = AN.\)

Mà \(G\) là trực tâm của tam giác \(\Delta BCD\) nên \(BG \bot CD\) tại \(N\) hay \(N\) là hình chiếu của \(B\) lên \(CD\).

Đáp án cần chọn là: c