Cho tứ diện $ABCD$ và điểm $M$ thuộc miền trong của tam giác $ACD\,.$ Gọi $I$ và $J$ lần lượt là hai điểm trên cạnh $BC$ và $BD$ sao cho $IJ$ không song song với $CD\,.$ Gọi $H,\,\,K$ lần lượt là giao điểm của $IJ$ với $CD$, của $MH$ và $AC\,.$ Giao tuyến của hai mặt phẳng $\left( {ACD} \right)$ và $\left( {IJM} \right)$ là:
Phương pháp giải
- Tìm giao điểm dễ thấy của hai mặt phẳng.
- Tìm giao điểm thứ hai bằng cách tìm hai đường thẳng nằm trong hai mặt phẳng mà cắt nhau.
Lời giải của Tự Học 365
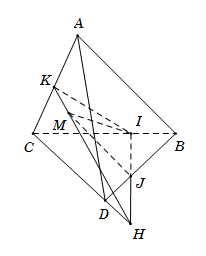
Trong mặt phẳng $\left( {BCD} \right),$ $IJ$ cắt $CD$ tại $H\,\, \Rightarrow \,\,H \in \left( {ACD} \right).$
Điểm $H \in IJ$ suy ra bốn điểm $M,\,\,I,\,\,J,\,\,H$ đồng phẳng.
Nên trong mặt phẳng $\left( {IJM} \right)$, $MH$ cắt $IJ$ tại $H$ và $MH \subset \left( {IJM} \right).$
Mặt khác $\left\{ \begin{array}{l}M \in \left( {ACD} \right)\\H \in \left( {ACD} \right)\end{array} \right.\,\, \Rightarrow \,\,MH \subset \left( {ACD} \right).$ Vậy $\left( {ACD} \right) \cap \left( {IJM} \right) = MH.$
Đáp án cần chọn là: d
Toán Lớp 12
