Lời giải của Tự Học 365

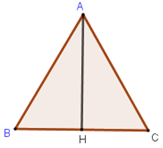
Tam giác \(ABC\) đều cạnh \(a\), trung điểm \(H\) của \(BC\) nên \(AC = AB = BC = a\) và \(BH = HC = \dfrac{a}{2}\).

Tam giác \(ABH\) vuông tại \(H\) nên \(A{H^2} + B{H^2} = A{B^2}\) \( \Rightarrow AH = \sqrt {A{B^2} - B{H^2}} \)\( = \sqrt {{a^2} - \dfrac{{{a^2}}}{4}}  = \dfrac{{a\sqrt 3 }}{2}\).

Do đó \(\left| {\overrightarrow {HB} } \right| = HB = \dfrac{a}{2}\) nên A đúng.

\(\left| {\overrightarrow {AH} } \right| = AH = \dfrac{{a\sqrt 3 }}{2}\) nên B đúng.

\(\left| {\overrightarrow {CH} } \right| = CH = \dfrac{a}{2}\) nên C sai.

\(\left| {\overrightarrow {BH} } \right| = \left| {\overrightarrow {HC} } \right| = \dfrac{a}{2}\) nên D đúng.

Đáp án cần chọn là: c