Lời giải của Tự Học 365

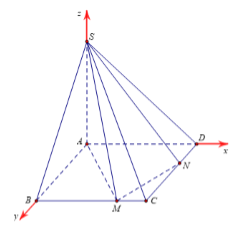
Chọn hệ trục tọa độ Axyz như hình vẽ.

Ta có: $A\left( {0;0;0} \right),{\mkern 1mu} S\left( {0;0;b} \right),{\mkern 1mu} M\left( {x;a;0} \right),{\mkern 1mu} N\left( {a;y;0} \right)$

$ \Rightarrow \overrightarrow {AM} \left( {x;a;0} \right),{\mkern 1mu} \overrightarrow {AS} \left( {0;0;b} \right)$

$ \Rightarrow $ Vtpt của $\left( {SAM} \right)$ là: $\overrightarrow {{n_1}}  = \left( {\overrightarrow {AM} ;{\mkern 1mu} \overrightarrow {AS} } \right) = \left( {ab; - bx;0} \right) = b\left( {a; - x;0} \right)$

$\overrightarrow {MS} \left( { - x; - a;b} \right),{\mkern 1mu} \overrightarrow {NS} \left( { - a; - y;b} \right)$

$ \Rightarrow $ vtpt của $\left( {SMN} \right)$ là: $\overrightarrow {{n_2}}  = \left( {\overrightarrow {MS} ;\overrightarrow {NS} } \right) = \left( {by - ab;bx - ab;xy - {a^2}} \right)$

Để hai mặt phẳng $(SAM)$ và $(SMN)$ vuông góc với nhau thì $\overrightarrow {{n_1}} .\overrightarrow {{n_2}}  = 0$

$ \Leftrightarrow a\left( {by - ab} \right) - x\left( {bx - ab} \right) + 0\left( {xy - {a^2}} \right) = 0$$ \Leftrightarrow {x^2} + {a^2} = a\left( {x + y} \right).$

Đáp án cần chọn là: b