Lời giải của Tự Học 365

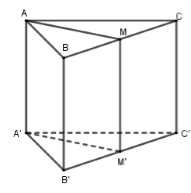
Phương trình \(BC \equiv Oz:\left\{ \begin{array}{l}x = 0\\y = 0\\z = t\end{array} \right.\).

Mặt phẳng \(\left( {AMM'A'} \right)\) đi qua \(A'\) và vuông góc với \(BC\) nên \(\left( {AMM'A'} \right)\) đi qua \(A'\left( {\sqrt 3 ; - 1;1} \right)\) và nhận \(\overrightarrow k  = \left( {0;0;1} \right)\) làm VTPT hay \(\left( {AMM'A'} \right):0\left( {x - \sqrt 3 } \right) + 0\left( {y + 1} \right) + 1\left( {z - 1} \right) = 0 \Leftrightarrow z = 1\).

\(M = BC \cap \left( {AMM'A'} \right) \Rightarrow t - 1 = 0 \Leftrightarrow t = 1 \Rightarrow M\left( {0;0;1} \right)\)

Mà \(AA' = 1,A'M = \sqrt {{{\left( {\sqrt 3  - 0} \right)}^2} + {{\left( { - 1 - 0} \right)}^2} + {{\left( {1 - 1} \right)}^2}}  = 2\) \( \Rightarrow AM = \sqrt {A'{M^2} - A'{A^2}}  = \sqrt {{2^2} - {1^2}}  = \sqrt 3 \).

Tam giác \(ABC\) đều có độ dài đường cao \(AM = \dfrac{{BC\sqrt 3 }}{2} = \sqrt 3  \Rightarrow BC = 2\)

Gọi \(B\left( {0;0;m} \right),C\left( {0;0;n} \right)\) với \(n e 0\) thì \(BC = 2 \Leftrightarrow \left| {m - n} \right| = 2\) và \(M\left( {0;0;1} \right)\) là trung điểm \(BC \Leftrightarrow \dfrac{{m + n}}{2} = 1 \Leftrightarrow m + n = 2\).

Khi đó \(m = 0,n = 2\) vì \(n e 0\) hay \(C\left( {0;0;2} \right)\).

\( \Rightarrow \overrightarrow {A'C}  = \left( { - \sqrt 3 ;1;1} \right)\) hay \(2\overrightarrow {AC'}  = \left( { - 2\sqrt 3 ;2;2} \right)\) là một VTCP của \(A'C\).

Suy ra \(a =  - 2\sqrt 3 ,b = 2 \Rightarrow {a^2} + {b^2} = {\left( { - 2\sqrt 3 } \right)^2} + {2^2} = 16\).

Đáp án cần chọn là: b