Lời giải của Tự Học 365

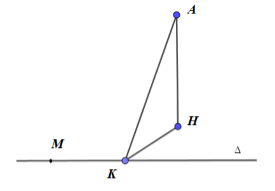
Do \(\Delta \) là đường thẳng đi qua \(M\left( {0;0;2} \right)\) và song song với mặt phẳng \(\left( P \right):x + y + z + 3 = 0\) \( \Rightarrow \Delta  \subset \left( Q \right)\): qua M và song song \(\left( P \right)\).

Phương trình mặt phẳng (Q) là: \(x + y + z - 2 = 0\).

Dựng \(AH \bot \left( Q \right),AK \bot \Delta \). Ta có: \(AK \ge AH\). Do đó, khoảng cách từ \(A\left( {5;0;0} \right)\) đến đường thẳng \(\Delta \) nhỏ nhất và bằng AH khi và chỉ khi K trùng H

Khi đó, đường thẳng \(\Delta \) được xác định là đường thẳng đi qua M và H.

Phương trình đường thẳng AH là \(\left\{ \begin{array}{l}x = 5 + t\\y = t\\z = t\end{array} \right. \Rightarrow \)Giả sử \(H\left( {5 + t;t;t} \right) \Rightarrow 5 + t + t + t - 2 = 0 \Leftrightarrow t =  - 1 \Rightarrow H\left( {4; - 1; - 1} \right)\)

\( \Rightarrow \overrightarrow {MH}  = \left( {4; - 1; - 3} \right) \Rightarrow \Delta \) có 1 VTCP là \(\overrightarrow {{u_3}}  = \left( {4; - 1; - 3} \right)\).

Đáp án cần chọn là: a