Lời giải của Tự Học 365

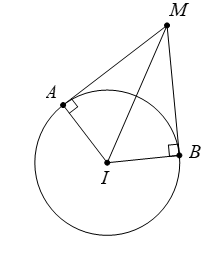
Xét \(\left( S \right):{{\left( x-1 \right)}^{2}}+{{\left( y-2 \right)}^{2}}+{{\left( z+1 \right)}^{2}}=6\) có tâm \(I\left( 1;2;-\,1 \right),\) bán kính \(R=\sqrt{6}.\)

Gọi \(M\) là giao điểm của \(\left( P \right)\) và \(\left( Q \right)\) sao cho \(MAIB\) đồng phẳng.

Ta có \(\cos \widehat{AMB}=\cos \widehat{\left( P \right);\left( Q \right)}=\frac{\left| {{{\vec{n}}}_{\left( P \right)}}.{{{\vec{n}}}_{\left( Q \right)}} \right|}{\left| {{{\vec{n}}}_{\left( P \right)}} \right|.\left| {{{\vec{n}}}_{\left( Q \right)}} \right|}=\frac{1}{2}\Rightarrow \,\,\widehat{AMB}={{60}^{0}}\Rightarrow \,\,\widehat{AIB}={{120}^{0}}.\)

Tam giác \(IAB\) cân tại \(I,\) có \(AB=\sqrt{I{{A}^{2}}+I{{B}^{2}}-2.IA.IB.\cos \widehat{AIB}}=3\sqrt{2}.\)

Đáp án cần chọn là: d