Cho $x,y$ thoả mãn hệ $\left\{ \begin{array}{l}x + 2y - 100 \le 0\\2x\,\, + \,y - 80\,\, \le 0\\x \ge 0\\y \ge 0\end{array} \right..$ Tìm giá trị lớn nhất \({P_{\max }}\) của biểu thức $P = \left( {x;y} \right) = 40000x + 30000y.$
Phương pháp giải
- Xác định miền nghiệm của hệ bất phương trình.
- Xác định tọa độ các đỉnh của đa giác giới hạn miền nghiệm.
- Tính giá trị của \(F\left( {x;y} \right)\) tại các điểm đó và kết luận.
Lời giải của Tự Học 365
Trong mặt phẳng tọa độ \(Oxy,\)vẽ các đường thẳng
\({d_1}:x + 2y - 100 = 0,\,\,{\rm{ }}{d_2}:2x + y - 80 = 0.\)
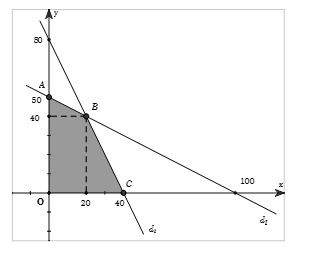
Khi đó miền nghiệm của hệ bất phương trình là phần mặt phẳng (tứ giác \(OABC\) kể cả biên) tô màu như hình vẽ.
Xét các đỉnh của miền khép kín tạo bởi hệ là
$\begin{array}{l}O\left( {0;0} \right),\,\,\\A\,\left( {0;50} \right),\,\,\\B\left( {20;40} \right),\\C\left( {40;0} \right).\end{array}$
Ta có \(\left\{ \begin{array}{l}P\left( {0;0} \right) = 0\\P\left( {0;50} \right) = 1500000\\P\left( {20;40} \right) = 2000000\\P\left( {40;0} \right) = 1600000\end{array} \right.\)
\( \Rightarrow {P_{\max }} = 2000000.\)
Đáp án cần chọn là: a
Toán Lớp 12
