Cho hệ bất phương trình \(\left\{ \begin{array}{l}x - y \le 2\\3x + 5y \le 15\\x \ge 0\\y \ge 0\end{array} \right.\). Khẳng định nào sau đây là khẳng định sai ?
Phương pháp giải
- Biểu diễn miền nghiệm của các bất phương trình trên cùng một hệ trục tọa độ.
- Xét tính đúng sai của từng đáp án và kết luận.
Lời giải của Tự Học 365
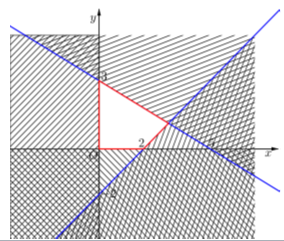
Trước hết, ta vẽ bốn đường thẳng:
\(\left( {{d_1}} \right):x - y = 2\)
\(\left( {{d_2}} \right):3x + 5y = 15\)
\(\left( {{d_3}} \right):x = 0\)
\(\left( {{d_4}} \right):y = 0\)
- Miền nghiệm là phần không bị gạch, kể cả biên nên A đúng.
- Đáp án B sai vì nếu \(m = 5\) ta vẽ đường thẳng \(x + y = 5\) sẽ không có giao điểm với miền nghiệm của hệ.
- Ta sẽ tìm GTLN, GTNN của biểu thức \(F\left( {x;y} \right) = x + y\) với \(\left( {x;y} \right)\) là nghiệm của hệ.
Ta có:
\(\begin{array}{l}F\left( {0;3} \right) = 0 + 3 = 3,F\left( {\dfrac{{25}}{8};\dfrac{9}{8}} \right) = \dfrac{{25}}{8} + \dfrac{9}{8} = \dfrac{{17}}{4},\\F\left( {2;0} \right) = 2 + 0 = 2,F\left( {0;0} \right) = 0 + 0 = 0\end{array}\)
Đáp án cần chọn là: b
Toán Lớp 12
