Cho hệ bất phương trình \(\left\{ \begin{array}{l}2x - \dfrac{3}{2}y \ge 1\\4x - 3y \le 2\end{array} \right.\) có tập nghiệm \(S\). Khẳng định nào sau đây là khẳng định đúng?
Phương pháp giải
- Biểu diễn miền nghiệm của hệ trên mặt phẳng tọa độ.
- Xét tính đúng, sai của từng đáp án và kết luận.
Lời giải của Tự Học 365
Dễ thấy \(x = - \dfrac{1}{4};y = - 1\) thỏa mãn cả hai bất phương trình nên \(\left( { - \dfrac{1}{4}; - 1} \right) \in S\), do đó A sai.
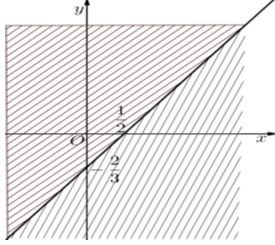
Ta sẽ biểu diễn tập nghiệm của bất phương trình trên mặt phẳng tọa độ như sau:
Trước hết, ta vẽ hai đường thẳng:
\(\left( {{d_1}} \right):2x - \dfrac{3}{2}y = 1\)
\(\left( {{d_2}} \right):4x - 3y = 2\)
Thử trực tiếp ta thấy \(\left( {0\,\,;\,\,0} \right)\) là nghiệm của phương trình (2) nhưng không phải là nghiệm của phương trình (1). Sau khi gạch bỏ các miền không thích hợp, tập hợp nghiệm của bất phương trình chính là các điểm thuộc đường thẳng \(\left( d \right):4x - 3y = 2.\)
Đáp án cần chọn là: b
Toán Lớp 12
