Lời giải của Tự Học 365

Xét phương trình: $\left| {2{x^2} - 3x - 2} \right| = 5a - 8x - {x^2}  \left( 1 \right)$

\( \Leftrightarrow 5a = f\left( x \right)\)\( = \left\{ \begin{array}{l}\left( {2{x^2} - 3x - 2} \right) + 8x + {x^2}{\rm{ khi }}2{x^2} - 3x - 2 \ge 0\\ - 2{x^2} + 3x + 2 + 8x + {x^2}\,\,{\rm{khi }}2{x^2} - 3x - 2 < 0\end{array} \right.\) \( = \left\{ \begin{array}{l}3{x^2} + 5x - 2 & {\rm{khi }}2{x^2} - 3x - 2 \ge 0\\ - {x^2} + 11x + 2 & {\rm{khi }}2{x^2} - 3x - 2 < 0\end{array} \right.\)

Bảng biến thiên:

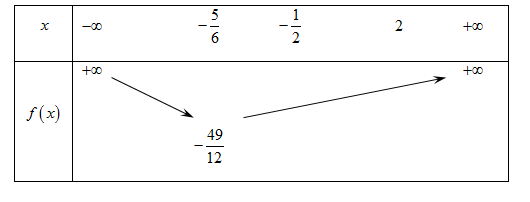
Dựa vào bảng biến thiên ta có: phương trình (1) có nghiệp duy nhất \(5a =  - \dfrac{{49}}{{12}} \Leftrightarrow a = \dfrac{{ - 49}}{{60}}\).

Đáp án cần chọn là: a