Lời giải của Tự Học 365

Bất phương trình $\dfrac{{{x^4} - {x^2}}}{{{x^2} + 5x + 6}} \le 0$ $ \Leftrightarrow \dfrac{{{x^2}\left( {{x^2} - 1} \right)}}{{{x^2} + 5x + 6}} \le 0\,\,\,\,\,\,\,\left(  *  \right)$

Vì ${x^2} \ge 0,\,\,\forall x \in \mathbb{R}$ nên bất phương trình

      $\left(  *  \right) \Leftrightarrow \left[ \begin{array}{l}{x^2} = 0\\\dfrac{{{x^2} - 1}}{{{x^2} + 5x + 6}} \le 0\end{array} \right.$ $ \Leftrightarrow \left[ \begin{array}{l}x = 0\\f\left( x \right) = \dfrac{{{x^2} - 1}}{{{x^2} + 5x + 6}} \le 0\end{array} \right.$

Phương trình ${x^2} - 1 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x =  - \,1\end{array} \right.$ và ${x^2} + 5x + 6 = 0 \Leftrightarrow \left[ \begin{array}{l}x =  - \,2\\x =  - \,3\end{array} \right..$

Bảng xét dấu

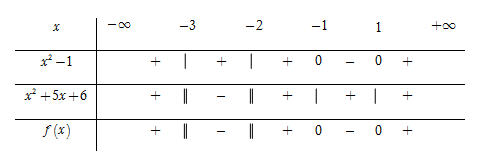
Dựa vào bảng xét dấu, ta thấy $f\left( x \right) \le 0 \Leftrightarrow x \in \left( { - \,3; - \,2} \right) \cup \left[ { - \,1;1} \right]$

Kết hợp với $x \in \mathbb{Z},$ ta được $x = \left\{ { - \,1;0;1} \right\}.$

Vậy có tất cả $3$ giá trị nguyên cần tìm.

Đáp án cần chọn là: d