Lời giải của Tự Học 365

Bất phương trình ${x^3} + 3{x^2} - 6x - 8 \ge 0 \Leftrightarrow \left( {x - 2} \right)\left( {{x^2} + 5x + 4} \right) \ge 0.$

Phương trình \({x^2} + 5x + 4 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x =  - \,4}\\{x =  - \,1}\end{array}} \right.\) và \(x - 2 = 0 \Leftrightarrow x = 2.\)

Lập bảng xét dấu

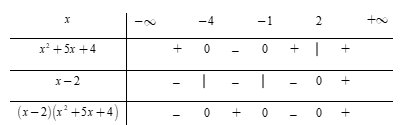
Dựa vào bảng xét dấu, ta thấy rằng $\left( {x - 2} \right)\left( {{x^2} + 5x + 4} \right) \ge 0 \Leftrightarrow x \in \left[ { - \,4; - \,1} \right] \cup \left[ {2; + \,\infty } \right).$

Đáp án cần chọn là: a