Để phương trình sau có 4 nghiệm phân biệt: \(\left| {10x - 2{x^2} - 8} \right| = {x^2} - 5x + a\) thì giá trị của tham số \(a\) là:
Phương pháp giải
- Cô lập \(a\) đưa về \(a = \left| {10x - 2{x^2} - 8} \right| - {x^2} + 5x\)
- Sử dụng phương pháp xét hàm số vế phải, lập bảng biến thiên suy ra giá trị của \(a\) để phương trình có \(4\) nghiệm.
Lời giải của Tự Học 365
Xét phương trình: \(\left| {10x - 2{x^2} - 8} \right| = {x^2} - 5x + a\) (1)
\( \Leftrightarrow a = \left| {10x - 2{x^2} - 8} \right| - {x^2} + 5x\)
Xét \(f\left( x \right) = \left| {10x - 2{x^2} - 8} \right| - {x^2} + 5x\)
\( = \left\{ \begin{array}{l}\left( {10x - 2{x^2} - 8} \right) - {x^2} + 5x{\rm{ }} & {\rm{khi }}10x - 2{x^2} - 8 \ge 0\\ - \left( {10x - 2{x^2} - 8} \right) - {x^2} + 5x{\rm{ }} & {\rm{khi }}10x - 2{x^2} - 8 < 0\end{array} \right.\)
\( = \left\{ \begin{array}{l} - 3{x^2} + 15x - 8 & {\rm{khi }}1 \le x \le 4\\{x^2} - 5x + 8 & {\rm{khi }}x \le 1 \vee x \ge 4\end{array} \right.\)
Bảng biến thiên:
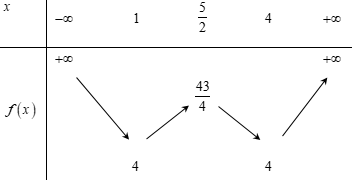
Dựa vào bảng biến thiên ta có phương trình (1) có 4 nghiệm phân biệt \( \Leftrightarrow 4 < a < \dfrac{{43}}{4}\).
Đáp án cần chọn là: d
Toán Lớp 12
