Lời giải của Tự Học 365

Điều kiện: \({x^2} - 3x - 10 e 0 \Leftrightarrow \left( {x + 2} \right)\left( {x - 5} \right) e 0 \Leftrightarrow \left\{ \begin{array}{l}x e  - \,2\\x e 5\end{array} \right..\)

Bất phương trình \(\dfrac{{ - \,2{x^2} + 7x + 7}}{{{x^2} - 3x - 10}} \le  - 1\)\( \Leftrightarrow \dfrac{{ - 2{x^2} + 7x + 7}}{{{x^2} - 3x - 10}} + 1 \le 0\) \( \Leftrightarrow \dfrac{{ - {x^2} + 4x - 3}}{{{x^2} - 3x - 10}} \le 0\,\,\,\,\left(  *  \right)\)

Bảng xét dấu

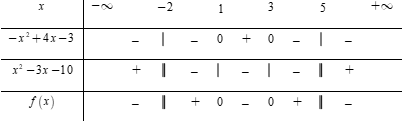
Dựa vào bảng xét dấu, bất phương trình \(\left(  *  \right) \Leftrightarrow x \in \left( { - \,\infty ; - \,2} \right) \cup \left[ {1;3} \right] \cup \left( {5; + \,\infty } \right).\)

Đáp án cần chọn là: c