Lời giải của Tự Học 365

Ta có $f\left( x \right) = {x^2} - 8x + 7 = 0\, \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 7\end{array} \right.$.

Bảng xét dấu

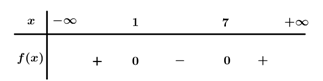
Dựa vào bảng xét dấu \(f\left( x \right) \ge 0\, \Leftrightarrow \,\left[ \begin{array}{l}x \le 1\\x \ge 7\end{array} \right.\).

Tập nghiệm của bất phương trình là \(S = \left( { - \infty ;1} \right] \cup \,\left[ {7; + \infty } \right)\).

Vì \(\dfrac{{13}}{2} \in \left[ {6; + \infty } \right)\) và \(\dfrac{{13}}{2} otin S\) nên \(\left[ {6; + \infty } \right)\) thỏa yêu cầu bài toán.

Đáp án cần chọn là: d