Lời giải của Tự Học 365

Ta có \(P = 7\left( {{x^4} + {y^4}} \right) + 4{x^2}{y^2}\)

\( = 7\left[ {\left( {{x^2} + {y^2}} \right) - 2{x^2}{y^2}} \right] + 4{x^2}{y^2}\)

\( = 7\left( {{x^2} + {y^2}} \right) - 10{x^2}{y^2}\)

\( = \dfrac{7}{4}{\left[ {2\left( {{x^2} + {y^2}} \right)} \right]^2} - 10{x^2}{y^2}\)

\( = \dfrac{7}{4}{\left( {1 + xy} \right)^2} - 10{x^2}{y^2} = \dfrac{7}{4} + \dfrac{7}{2}xy - \dfrac{{33}}{4}{\left( {xy} \right)^2}\)

Theo giả thiết, \(2\left( {{x^2} + {y^2}} \right) = 1 + xy \Rightarrow 2\left[ {{{\left( {x + y} \right)}^2} - 2xy} \right] = 1 + xy\)

\( \Rightarrow 5xy + 1 = 2{\left( {x + y} \right)^2} \ge 0 \Rightarrow xy \ge  - \dfrac{1}{5}\,\,\left( * \right)\)

Lại có \(2\left( {{x^2} + {y^2}} \right) \ge 4xy \Rightarrow 1 + xy \ge 4xy \Rightarrow xy \le \dfrac{1}{3}\,\,\left( {**} \right)\)

Từ \(\left( * \right)\) và \(\left( {**} \right)\) suy ra \(xy \in \left[ { - \dfrac{1}{5};\dfrac{1}{3}} \right]\).

Đặt \(t = xy\), suy ra \(t \in \left[ { - \dfrac{1}{5};\dfrac{1}{3}} \right]\).

Khi đó \(P =  - \dfrac{{33}}{4}{t^2} + \dfrac{7}{2}t + \dfrac{7}{4}\) với \(t \in \left[ { - \dfrac{1}{5};\dfrac{1}{3}} \right]\).

Ta có bảng biến thiên:

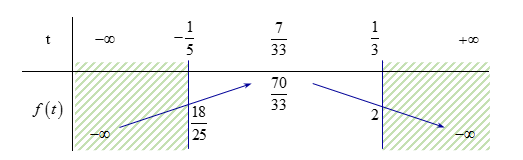
Dựa vào bảng biến thiên, suy ra GTLN của \(P\) là \(M = \dfrac{{70}}{{33}}\) và GTNN của \(P\) là \(m = \dfrac{{18}}{{25}}\).

Vậy \(M + m = \dfrac{{18}}{{25}} + \dfrac{{70}}{{33}} = \dfrac{{2344}}{{825}}\).

Đáp án cần chọn là: d