Cho tứ diện \(ABCD.\) Gọi \(M,{\rm{ }}N\) lần lượt là trung điểm của \(AB\) và \(CD.\) Mặt phẳng \(\left( \alpha \right)\) qua \(MN\) cắt \(AD,{\rm{ }}BC\) lần lượt tại \(P\) và \(Q.\) Biết \(MP\) cắt \(NQ\) tại \(I.\) Ba điểm nào sau đây thẳng hàng?
Phương pháp giải
Sử dụng định lý: Ba mặt phẳng cắt nhau theo ba giao tuyến phân biệt, nếu chúng không song song thì đồng qui.
Lời giải của Tự Học 365
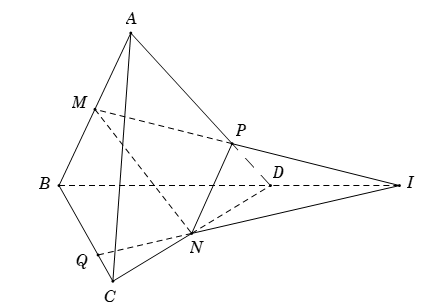
Ta có \(\left( {ABD} \right) \cap \left( {BCD} \right) = BD\).
Lại có \(\left\{ \begin{array}{l}I \in MP \subset \left( {ABD} \right)\\I \in NQ \subset \left( {BCD} \right)\end{array} \right. \Rightarrow I\) thuộc giao tuyến của \(\left( {ABD} \right)\) và \(\left( {BCD} \right)\)
\( \Rightarrow I \in BD \Rightarrow I,{\rm{ }}B,{\rm{ }}D\) thẳng hàng.
Đáp án cần chọn là: b
Toán Lớp 12
