Cho hình chóp tứ giác đều \(S.ABCD\) có cạnh đáy bằng \(a\,\,\,\,\left( {a > 0} \right).\) Các điểm \(M,\,\,N,\,\,P\) lần lượt là trung điểm của \(SA,\,\,SB,\,\,SC\,.\) Mặt phẳng \(\left( {MNP} \right)\) cắt hình chóp theo một thiết diện có diện tích bằng:
Phương pháp giải
- Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng \(\left( {MNP} \right)\).
- Nhận dạng thiết diện và tính diện tích.
Lời giải của Tự Học 365
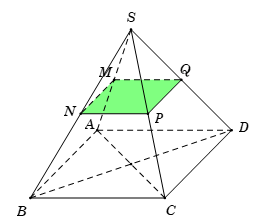
Gọi \(Q\) là trung điểm của \(SD\,.\)
Tam giác \(SAD\) có \(M,\,\,Q\) lần lượt là trung điểm của \(SA,\,\,SD\) suy ra \(MQ\)//\(AD\,.\)
Tam giác \(SBC\) có \(N,\,\,P\) lần lượt là trung điểm của \(SB,\,\,SC\) suy ra \(NP\)//\(BC\,.\)
Mặt khác \(AD//BC\) suy ra \(MQ\)//\(NP\) và \(MQ = NP\,\, \Rightarrow \,\,MNPQ\) là hình vuông.
Khi đó \(M,\,\,N,\,\,P,\,\,Q\) đồng phẳng \( \Rightarrow \,\,\left( {MNP} \right)\) cắt \(SD\) tại \(Q\,\) và \(MNPQ\) là thiết diện của hình chóp \(S.ABCD\) với \(mp\,\,\left( {MNP} \right).\)
Lại có \(\dfrac{{NP}}{{BC}} = \dfrac{1}{2} \Rightarrow \dfrac{{{S_{MNPQ}}}}{{{S_{ABCD}}}} = {\left( {\dfrac{1}{2}} \right)^2} = \dfrac{1}{4}\).
Vậy diện tích hình vuông \(MNPQ\) là \({S_{MNPQ}} = \dfrac{{{S_{ABCD}}}}{4} = \dfrac{{{a^2}}}{4}.\)
Đáp án cần chọn là: c
Toán Lớp 12
