Câu hỏi
Vận dụng
Cho tứ diện $ABCD.$ Gọi $M, N$ lần lượt là trung điểm của các cạnh $AD $ và $ BC, G$ là trọng tâm tam giác $BCD.$ Khi đó giao điểm của đường thẳng $MG$ và $mp(ABC)$ là:
Đáp án đúng: b
Phương pháp giải
Đừa về cùng mặt phẳng. Tìm trong mặt phẳng $(SAB)$ một đường thẳng cắt $DY.$ Giao điểm của đường thẳng đó và $SO$ chính là giao điểm của $(SAB)$ và $DY.$
Lời giải của Tự Học 365
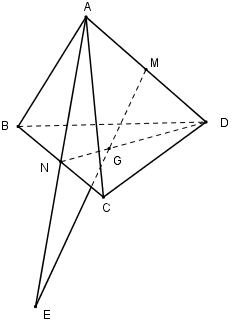
Ta có: \(\dfrac{{DM}}{{DA}} e \dfrac{{DG}}{{DN}}\,\,\left( {\dfrac{1}{2} e \dfrac{2}{3}} \right) \)
\(\Rightarrow \) $MG$ và $AN$ không song song với nhau.
Trong $(ADN)$ gọi \(E = MG \cap AN.\) Mà \(AN \subset \left( {ABC} \right) \Rightarrow MG \cap \left( {ABC} \right) = E.\)
Đáp án cần chọn là: b
Toán Lớp 12
