Câu hỏi
Vận dụng
Cho hình chóp $S.ABC.$ $M, N$ lần lượt là trung điểm $SA, AB.$ $P$ nằm trên cạnh $BC$ sao cho $BP = 2PC.$ Giao điểm $I$ của $SC$ và $(MNP)$ là:
Đáp án đúng: c
Phương pháp giải
+ Tìm một mặt phẳng thích hợp chứa $SC$
+ Tìm giao tuyến của mặt phẳng đó với $(MNP)$
+ Tìm giao điểm của giao tuyến đó với $SC$
Lời giải của Tự Học 365
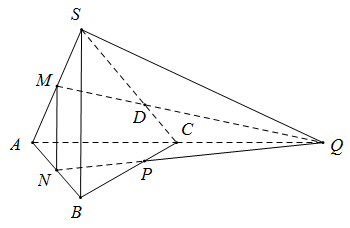
Có $SC ⊂ (SAC)$
Gọi $Q$ là giao điểm của $NP$ và $AC$
$⇒ (MNP) ∩ (SAC) = MQ$
Gọi $D$ là giao $MQ $ và $SC$
$⇒ D$ là giao của $SC$ và $(MNP)$
Vậy $D \equiv I$ hay $I$ là giao điểm của $MQ$ và $SC$ (với $Q$ là giao điểm của $AC$ với $NP$)
Đáp án cần chọn là: c
Toán Lớp 12
