Cho tứ diện \(ABCD\,.\) Gọi \(M,\,\,N\) lần lượt là trung điểm các cạnh \(AB\) và \(AC,\) \(E\) là điểm trên cạnh \(CD\) với \(ED = 3EC.\) Thiết diện tạo bởi mặt phẳng \(\left( {MNE} \right)\) và tứ diện \(ABCD\) là:
Phương pháp giải
Sử dụng định lý ba giao tuyến song song: Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến, nếu có hai đường thẳng song song thì đường thẳng thứ ba cũng song song với chúng.
Lời giải của Tự Học 365
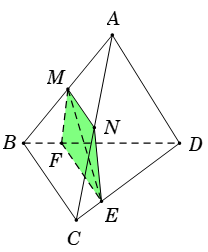
Tam giác \(ABC\) có \(M,\,\,N\) lần lượt là trung điểm của \(AB,\,\,AC\,.\)
Suy ra \(MN\) là đường trung bình của tam giác \(ABC\) \( \Rightarrow \,\,MN\)//\(BC\,.\)
Từ \(E\) kẻ đường thẳng \(d\) song song với \(BC\) và cắt \(BD\) tại \(F\,\, \Rightarrow \,\,EF\)//\(BC.\)
Do đó \(MN//EF\) suy ra bốn điểm \(M,\,\,N,\,\,E,\,\,F\) đồng phẳng và \(MNEF\) là hình thang.
Vậy hình thang \(MNEF\) là thiết diện cần tìm.
Đáp án cần chọn là: d
Toán Lớp 12
