Cho chóp tứ giác $S.ABCD$ có hai đường chéo $AC$ và $BD$. Gọi $E$ và $F$ lần lượt là giao điểm của $AB$ và $CD,AD$ và $BC$ . Một mặt phẳng \(\left( \alpha \right)\) đi qua điểm $M$ trên cạnh $SB$ ($M$ nằm giữa $S$ và $B$ ) song song với $SE$ và $SF$ ($SE$ không vuông góc với $SF$). Thiết diện của hình chóp cắt bởi \(mp\left( \alpha \right)\) có số cạnh là:
Phương pháp giải
- Đưa về cùng mặt phẳng.
- Sử dụng các yếu tố song song.
- Xác định thiết diện của hình chóp dựa vào các yếu tố song song.
Lời giải của Tự Học 365
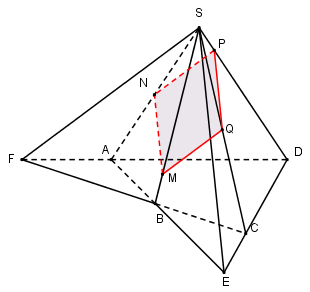
Giả sử thiết diện cần tìm đi qua điểm \(M \in SB.\)
Trong $\left( {SAB} \right)$ qua $M$ kẻ \(MN//SE\left( {N \in SA} \right)\) ta có:
\(\left( \alpha \right)\) và $\left( {SAB} \right)$ có điểm $M$ chung.
\(\begin{array}{l}\left( \alpha \right)//SE \subset \left( {SAB} \right)\\MN//SE\\ \Rightarrow \left( \alpha \right) \cap \left( {SAB} \right) = MN.\end{array}\)
Tương tự trong $\left( {SAD} \right)$ qua $N$ kẻ \(NP//SF\left( {P \in SD} \right)\) ta có: \(\left( \alpha \right) \cap \left( {SAD} \right) = NP.\)
Trong $\left( {SCD} \right)$ kẻ \(PQ//SE\left( {Q \in SC} \right)\) ta có: \(\left( \alpha \right) \cap \left( {SCD} \right) = PQ.\)
\(\left( \alpha \right) \cap \left( {SBC} \right) = MQ.\)
Vậy thiết diện của hình chóp khi cắt bởi \(mp\left( \alpha \right)\) là tứ giác $MNPQ$.
Đáp án cần chọn là: b
Toán Lớp 12
