Cho hai số phức \({z_1},{z_2}\) thỏa mãn \(\left| {{z_1}} \right| = 6,\left| {{z_2}} \right| = 2\). Gọi \(M,N\) lần lượt là các điểm biểu diễn của số phức \({z_1}\) và số phức \(i{z_2}\). Biết \(\widehat {MON} = {60^0}\). Tính \(T = \left| {z_1^2 + 9z_2^2} \right|\).
Phương pháp giải
Chọn điểm rơi: cho số phức \({z_1}\) nhận một giá trị đặc biệt, tìm \({z_2}\) rồi thay vào tìm \(T\).
Lời giải của Tự Học 365
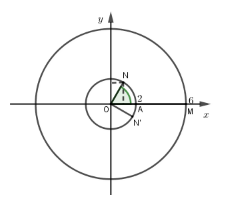
Ta chọn \({z_1} = 6\) có điểm biểu diễn là \(M\left( {6;0} \right)\).
Khi đó \(\widehat {MON} = {60^0}\) nên chọn \(N\left( {1;\sqrt 3 } \right)\) (hình vẽ) biểu diễn số phức \(i{z_2}\)
Suy ra điểm \(N'\left( {\sqrt 3 ; - 1} \right)\) biểu diễn số phức \({z_2}\) hay \({z_2} = \sqrt 3 - i\).
Khi đó \(T = \left| {z_1^2 + 9z_2^2} \right| = \left| {{6^2} + 9{{\left( {\sqrt 3 - i} \right)}^2}} \right| = 36\sqrt 3 \).
Đáp án cần chọn là: b
Toán Lớp 12
