Số phức \(z\) được biểu diễn trên trên mặt phẳng như hình vẽ.
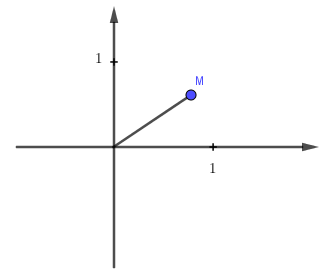
Hỏi hình nào biểu diễn cho số phức $w = \dfrac{i}{{\overline z }}$
Phương pháp giải
- Gọi số phức \(z = a + bi\) có điểm biểu diễn là \(M\left( {a;b} \right)\). Từ hình vẽ suy ra điều kiện của \(a,b\).
- Tính số phức \(w\) dựa vào các phép tính cộng, trừ, nhân, chia số phức.
- Đánh giá phần thực và phần ảo của \(w\) và suy ra đáp án cần tìm.
Lời giải của Tự Học 365
Giả sử $z = a + bi$ với $0 < a,b < 1$.
Có $w = \dfrac{i}{{\overline z }} = \dfrac{i}{{a - bi}} = \dfrac{{i(a + bi)}}{{{a^2} + {b^2}}} = \dfrac{{ - b}}{{{a^2} + {b^2}}} + \dfrac{{ai}}{{{a^2} + {b^2}}}$
Vì $z$ thuộc góc phần tư thứ I nên \( - \dfrac{b}{{{a^2} + {b^2}}} < 0;\dfrac{a}{{{a^2} + {b^2}}} > 0\). Do đó $w$ thuộc góc phần tư thứ II.
Đáp án cần chọn là: b
Toán Lớp 12
