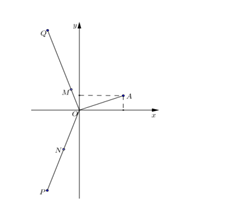
Cho số phức $z$ thỏa mãn $\left| z \right| = \dfrac{{\sqrt 2 }}{2}$ và điểm $A$ trong hình vẽ bên là điểm biểu diễn của $z$. Biết rằng trong hình vẽ bên, điểm biểu diễn của số phức $w = \dfrac{1}{{iz}}$ là một trong bốn điểm $M,N, P, Q$. Khi đó điểm biểu diễn của số phức $w$ là
Phương pháp giải
Cho số phức $z = a + bi \Rightarrow \left| z \right| = \sqrt {{a^2} + {b^2}} $
Với \(a,b > 0\) thì:
- Điểm biểu diễn của $z$ nằm trong góc phần tư thứ nhất là: $z = a + bi$
- Điểm biểu diễn của $z$ nằm trong góc phần tư thứ hai là: $z = - a + bi$
- Điểm biểu diễn của $z$ nằm trong góc phần tư thứ nhất là: $z = - a - bi$
- Điểm biểu diễn của $z$ nằm trong góc phần tư thứ nhất là: $z = a - bi$
Lời giải của Tự Học 365
Do điểm $A$ là điểm biểu diễn của $z$ nằm trong góc phần tư thứ nhất của mặt phẳng $Oxy$ nên gọi $z = a + bi\left( {a,b > 0} \right)$
Do $\left| z \right| = \dfrac{{\sqrt 2 }}{2} \Rightarrow \sqrt {{a^2} + {b^2}} = \dfrac{{\sqrt 2 }}{2}$
Lại có: \({\text{w}} = \dfrac{1}{{iz}} = \dfrac{{ - b}}{{{a^2} + {b^2}}} - \dfrac{a}{{{a^2} + {b^2}}}i\) .
$\left| {\rm{w}} \right| = \left| {\dfrac{1}{{iz}}} \right| = \dfrac{1}{{\left| i \right|.\left| z \right|}} = \sqrt 2 = 2\left| z \right| = 2OA$
Vậy điểm biểu diễn của số phức $w$ là điểm $P$.
Đáp án cần chọn là: d
Toán Lớp 12
