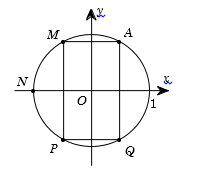
Cho số phức \(z\) thỏa mãn \(\left| z \right| = 1\) và điểm \(A\) trong hình vẽ bên là điểm biểu diễn của \(z\). Biết rằng trong hình vẽ bên, điểm biểu diễn của số phức $w = \dfrac{1}{z}$ là một trong bốn điểm \(M,{\rm{ }}N,{\rm{ }}P,{\rm{ }}Q\). Khi đó điểm biểu diễn của số phức $w$ là
Phương pháp giải
Tìm số phức \(w\) và đối chiếu vị trí của các điểm.
Lời giải của Tự Học 365
Gọi \(z = x + yi{\rm{ }}\left( {x;{\rm{ }}y \in \mathbb{R}} \right)\) được biểu diễn bởi \(A\).
Từ giả thiết, ta có \(\left\{ \begin{array}{l}{x^2} + {y^2} = 1\\x > 0;{\rm{ }}y > 0\end{array} \right..\)
Ta có \(w = \dfrac{1}{z} = \dfrac{1}{{x + yi}} = \dfrac{{x - yi}}{{{x^2} + {y^2}}} = x - yi = \bar z\).
Vì hai số phức \(z\) và \(\bar z\) có điểm biểu diễn đối xứng qua trục hoành nên ta chọn điểm \(Q\) thỏa mãn yêu cầu bài toán.
Đáp án cần chọn là: b
Toán Lớp 12
