Câu hỏi
Thông hiểu
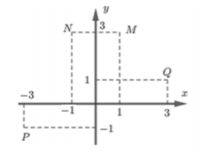
Điểm nào trong hình vẽ dưới đây là biểu diễn hình học của số phức \(z = \left( { - 1 - 2i} \right)\left( {3 + i} \right) - 2 + 6i?\)
Đáp án đúng: a
Phương pháp giải
- Rút gọn tìm số phức \(z\).
- Điểm \(M\left( {a;b} \right)\) biểu diễn số phức \(z = a + bi\).
Lời giải của Tự Học 365
Ta có : \(z = \left( { - 1 - 2i} \right)\left( {3 + i} \right) - 2 + 6i\) \( = - 3 - 6i - i - 2{i^2} - 2 + 6i = - 3 - i\).
Do đó \(z = - 3 - i \Rightarrow P\left( { - 3; - 1} \right)\) biểu diễn số phức \(z\).
Đáp án cần chọn là: a
Toán Lớp 12
