. Từ một điểm M nằm ngoài đường tròn (O), kẻ hai tiếp tuyến MA và MB c

Câu hỏi
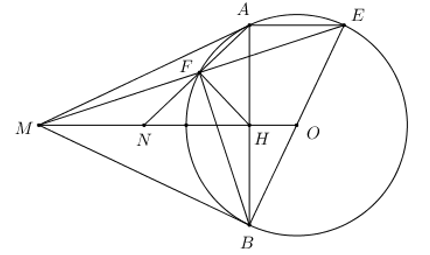
Nhận biếtCho đường tròn (O). Từ một điểm M nằm ngoài đường tròn (O), kẻ hai tiếp tuyến MA và MB của đường tròn (A, B là các tiếp điểm). Kẻ đường kính BE của đường tròn (O). Gọi F là giao điểm thứ hai của ME và đường tròn (O). Đường thẳng AF cắt MO tại điểm N. Gọi H là giao điểm của MO và AB.
1) Chứng minh tứ giác MAOB nội tiếp đường tròn.
2) Chứng minh đường thẳng AE song song với đường thẳng MO.
3) Chứng minh \(M{N^2} = NF.NA\)
4) Chứng minh \(MN = NH\)
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
1) Do MA, MB là các tiếp tuyến của (O)
\( \Rightarrow OA \bot MA;\,\,OB \bot MB \Rightarrow \widehat {OAM} = \widehat {OBM} = {90^0}\)
Xét tứ giác OAMB có \(\widehat {OAM} + \widehat {OBM} = {180^0}\)
\( \Rightarrow \) Tứ giác OAMB là tứ giác nội tiếp. (dhnb)
2) \(\widehat {EAB}\) là tứ giác nội tiếp chắn nửa đường tròn (O) \( \Rightarrow \widehat {EAB} = {90^0} \Rightarrow AE \bot AB\)
Mà \(MO \bot AB\) (tính chất hai tiếp tuyến cắt nhau)
\( \Rightarrow AE//MO\) (cùng vuông góc với AB).
3) Ta có \(\widehat {AFE} = \widehat {ABE}\) (hai góc nội tiếp cùng chắn cung AE)
\(\widehat {ABE} = \widehat {OMB}\) (cùng phụ \(\widehat {MBH}\))
\(\widehat {OMB} = \widehat {OMA}\) (tính chất hai tiếp tuyến cắt nhau)
\( \Rightarrow \widehat {AFE} = \widehat {OMA}\)
Lại có \(\widehat {AFE} = \widehat {MFN}\) (đối đỉnh) \( \Rightarrow \widehat {MFN} = \widehat {OMA}\)
Xét \(\Delta MNF\) và \(\Delta ANM\) có \(\widehat {ANM}\) chung, $\widehat{MFN}=\widehat{OMA}\,\,\,\left( cmt \right)\Rightarrow \Delta MNF\backsim \Delta ANM\,\,\left( g.g \right)$
\( \Rightarrow \frac{{MN}}{{NA}} = \frac{{NF}}{{MN}} \Rightarrow M{N^2} = NF.NA\,\,\,\left( 1 \right)\)
d) $\Delta MNF\backsim \Delta ANM\ \ \left( g-g \right)\Rightarrow \widehat{FMN}=\widehat{MAN}$ (hai góc tương ứng).
Mà \(\widehat {MAN} = \widehat {ABF}\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung AF)
\( \Rightarrow \widehat {FMN} = \widehat {ABF} \Rightarrow \) Tứ giác BHFM là tứ giác nội tiếp (tứ giác có hai góc nội tiếp cùng chắn một cung bằng nhau).
\( \Rightarrow \widehat {MFB} = \widehat {MHB}\) (hai góc nội tiếp cùng chắn cung MB). Mà \(\widehat {MHB} = {90^0}\) (tính chất hai tiếp tuyến cắt nhau)
\( \Rightarrow \widehat {MFB} = {90^0} \Rightarrow \widehat {MFN} + \widehat {NFB} = {90^0}\).
Tứ giác BHFM nội tiếp (cmt) \( \Rightarrow \widehat {BFH} = \widehat {BMH}\) (hai góc nội tiếp cùng chắn cung BH).
Mà \(\widehat {MFN} = \widehat {OMA}\,\,\left( {cmt} \right);\,\,\widehat {OMA} = \widehat {BMH} \Rightarrow \widehat {MFN} = \widehat {BMH}\)
\( \Rightarrow \widehat {BFH} = \widehat {MFN}\)
\( \Rightarrow \widehat {BFH} + \widehat {NFB} = {90^0} \Rightarrow \widehat {NFH} = {90^0}\)
Xét \(\Delta NFH\) và \(\Delta NHA\) có \(\widehat {ANH}\) chung, \(\widehat {NFH} = \widehat {NHA} = {90^0}\)
$\Rightarrow \Delta NFH\backsim \Delta NHA\,\,\left( g.g \right)\Rightarrow \frac{NF}{NH}=\frac{NH}{NA}\Rightarrow N{{H}^{2}}=NF.NA\,\,\,\left( 2 \right)$
Từ (1) và (2) \( \Rightarrow MN = NH\).


