Góc tạo bởi hai tia phân giác của hai góc kề bù bằng bao nhiêu? Vì sao?
Câu hỏi
Nhận biếtGóc tạo bởi hai tia phân giác của hai góc kề bù bằng bao nhiêu? Vì sao?
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
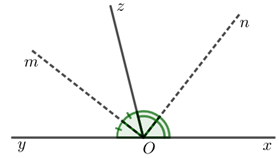
Gọi \(On\) và \(Om\) là tia phân giác của hai góc kề bù \(\angle xOz\) và \(\angle zOy\).
* \(On\) là tia phân giác của \(\angle xOz\), ta có:
+) Tia \(On\) nằm giữa hai tia \(Ox\) và \(Oz\)
+) \(\angle xOn = \angle nOz = \frac{{\angle xOz}}{2} \Rightarrow \angle xOz = 2\angle nOz\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\)
* \(Om\) là tia phân giác của góc \(\angle yOz,\) ta có:
+) Tia \(Om\) nằm giữa hai tia \(Oy\) và \(Oz\)
+) \(\angle yOm = \angle mOz = \frac{{\angle yOz}}{2} \Rightarrow \angle yOz = 2\angle mOz\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\)
* Vì \(\angle xOz\) và \(\angle zOy\) là hai góc kề bù nên ta có: \(\angle xOz + \angle zOy = {180^0}\,\,\,\,\,\,\,\,\,\,\left( 3 \right)\)
Thay \(\left( 1 \right)\) và \(\left( 2 \right)\) vào \(\left( 3 \right)\) ta có:
\(2\angle nOz + 2\angle mOz = {180^0}\)
\( \Rightarrow 2.\left( {\angle nOz + \angle mOz} \right) = {180^0}\)
\( \Rightarrow \angle nOz + \angle mOz = {180^0}:2\)
\( \Rightarrow \angle nOz + \angle mOz = {90^0}\)
* Ta có:
+) Tia \(On\) nằm giữa hai tia \(Ox\) và \(Oz\)
+) Tia \(Om\) nằm giữa hai tia \(Oy\) và \(Oz\)
+) Tia \(Oz\) nằm giữa hai tia \(Ox\) và \(Oy\)
\( \Rightarrow \) Tia \(Oz\) nằm giữa hai tia \(On\) và \(Om\)
\( \Rightarrow \angle nOz + \angle zOm = \angle nOm\) mà \(\angle nOz + \angle zOm = {90^0}\)
\( \Rightarrow \angle nOm = {90^0}\)
Vậy góc tạo bởi các tia phân giác của hai góc kề bù là góc vuông.
Chọn B.
Luyện tập
Câu hỏi liên quan
-
Tìm \(4\) số tự nhiên liên tiếp mà tổng bằng \(2010.\)
-
Phép toán \({6^2}:4.3 + {2.5^2}\) có kết quả là:
-
Biết \({5^{x - 3}} = 25\) . Giá trị của \(x\) là:
-
Tính bằng cách hợp lí (nếu có thể) :
\(\begin{array}{*{20}{l}}{A = \left( {6888:56-{{11}^2}} \right).152 + 13.72 + 13.28}\\{B = \left[ {5082:\left( {{{17}^{29}}:{{17}^{27}}-{{16}^2}} \right) + 13.12} \right]:31 + {9^2}}\end{array}\)
-
Viết liên tiếp các số từ \(1\) đến \(9999\) ta được số \(123…99999\). Tìm tổng các chữ số của số đó.
-
Tìm \(x\):
\(a)\,\,\,\,{\left( {7x - 11} \right)^3} = {2^5}{.5^2} + 200\)
\(b)\,\,\,\,\,{5^{x - 2}} - {3^2} = {2^4} - \left( {{6^8}:{6^6} - {6^2}} \right)\)
-
Theo kế hoạch hai tổ sản xuất \(600\) sản phẩm. Do cải tiến kĩ thuật nên tổ \(I\) đã vượt mức \(18\% \) và tổ \(II\) vượt mức \(21\% \) . Vì vậy trong thời gian quy định họ đã hoàn thành vượt mức \(120\) sản phẩm. Hỏi sản phẩm tổ \(I\) và tổ \(II\) được giao theo kế hoạch là bao nhiêu?
-
Tìm \(x\) biết:
\(\begin{array}{l}a)\;\left( {2x-130} \right):4 + 213 = {5^2} + 193\\b)\left( {{5^2} + {3^2}} \right)x + \left( {{5^2}-{3^2}} \right)x-50 = {10^2}\end{array}\)
-
Viết kết quả của phép tính \({27^{16}}:{9^{10}}\) dưới dạng lũy thừa:
-
Cách tính đúng của phép tính \({4^4}:{4^3}\) là: