Quy tắc xét dấu biểu thức và bài tập minh họa

Quy tắc xét dấu biểu thức (bài tập minh họa)

3 Bước để xét dấu

Để xét dấu cho biểu thức $g\left( x \right)=\frac{p\left( x \right)}{q\left( x \right)}$  ta làm như sau:

- Bước 1: Điều kiện: $q\left( x \right)\ne 0$.

Tìm tất cả các nghiệm của $p\left( x \right)\text{; }q\left( x \right)$và sắp xếp các nghiệm đó theo thứ tự tăng dần và điền vào trục số Ox.

- Bước 2: Cho $x\to +\infty$ để xác định dấu cùa $g\left( x \right)$ khi $x\to +\infty$.

- Bước 3: Xác định dấu của các khoảng còn lại dựa vào quy tắc sau:

Chú ý: Qua nghiệm bội lẻ thì $g\left( x \right)$ đổi dấu còn qua nghiệm bội chẵn thì $g\left( x \right)$ không đổi dấu (chẵn giữ nguyên, lẻ đổi dấu).

Bài tập minh họa

Ví dụ: Xét dấu của biểu thức $f\left( x \right)=\frac{\left( x-4 \right).{{\left( x-5 \right)}^{4}}}{\left( x+2 \right){{\left( x+1 \right)}^{2}}}$.

Bước 1: Ta thấy nghiệm của biểu thức trên là $-2;-1;4;5$ sắp xếp thứ tự tăng dần trên trục số.

Bước 2: Khi $x\to +\infty$ (ví dụ cho x = 10000) ta thấy $f\left( x \right)$ nhận giá trị dương.

Bước 3: Xác định dấu cùa các khoảng còn lại. Do ${{\left( x-5 \right)}^{4}}$ mũ chẵn (nghiệm bội chẵn) nên qua 5 biểu thức không đổi dấu. Do ${{\left( x-4 \right)}^{1}}$mũ lẻ (nghiệm bội lẻ) nên qua 4 biểu thức đổi dấu ...

Ta được bảng xét dấu cùa $f\left( x \right)$ như sau:

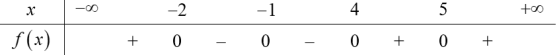
Kết luận: $f\left( x \right)>0\Leftrightarrow x\in \left( -\infty ;-2 \right)\cup \left( 4;5 \right)\cup \left( 5;+\infty  \right)$ và $f\left( x \right)<0\Leftrightarrow x\in \left( -2;-1 \right)\cup \left( -1;4 \right)$.