Giải PT Logarit bằng phương pháp đánh giá, hàm số có đáp án chi tiết

Giải PT Logarit bằng phương pháp đánh giá, hàm số có đáp án chi tiết

Kiến thức cần nhớ:

Hàm số $y=f\left( x \right)$ đồng biến (hoặc nghịch biến trên $\mathbb{R}$) thì phương trình $f\left( x \right)=f\left( {{x}_{0}} \right)\Leftrightarrow x={{x}_{0}}.$

Hàm số $f\left( t \right)$ đồng biến hoặc nghịch biến trên D (trong đó D là một khoảng, một đoạn, một nửa đoạn) thì với $u;v\in D$ ta có: $f\left( u \right)=f\left( v \right)\Leftrightarrow u=v.$

Một số bài tập, bài tập trắc nghiệm giải phương trình logarit

Lời giải:

a) Điều kiện: $\frac{2{{x}^{2}}+1}{{{x}^{2}}+x+1}>0\Leftrightarrow x\in \mathbb{R}.$

Khi đó $PT\Leftrightarrow \ln \left( 2{{x}^{2}}+1 \right)-\ln \left( {{x}^{2}}+x+1 \right)=\left( 2{{x}^{2}}+1 \right)-\left( {{x}^{2}}+x+1 \right)$

$\Leftrightarrow \ln \left( 2{{x}^{2}}+1 \right)+2{{x}^{2}}+1=\ln \left( {{x}^{2}}+x+1 \right)+\left( {{x}^{2}}+x+1 \right)$

Xét hàm số $f\left( t \right)=\ln t+t\,\,\left( t>0 \right)$ ta có: $f'\left( t \right)=\frac{1}{t}+1>0\,\,\left( \forall t\in \mathbb{R} \right)$ suy ra hàm số$f\left( t \right)$đồng biến trên $\mathbb{R}$nên $f\left( 2{{x}^{2}}+1 \right)=f\left( {{x}^{2}}+x+1 \right)\Leftrightarrow 2{{x}^{2}}+1={{x}^{2}}+x+1\Leftrightarrow {{x}^{2}}=x\Leftrightarrow \left[ \begin{array}  {} x=0 \\  {} x=1 \\ \end{array} \right..$

b) Đáp số: $x=-2;x=-1.$

Lời giải:

a) Điều kiện: $x>-\frac{1}{6}$. Đặt $y={{\log }_{7}}\left( 6x+1 \right)$ ta có: $6x+1={{7}^{y}}$ và ${{7}^{x}}-1=6y$

Suy ra \[\left\{ \begin{align} & {{7}^{x}}=6y+1 \\ & {{7}^{y}}=6x+1 \\ \end{align} \right.\Rightarrow {{7}^{x}}-{{7}^{y}}=6y-6x\Leftrightarrow {{7}^{x}}+6x={{7}^{y}}+6y\]

Xét hàm số $f\left( t \right)={{7}^{t}}+6t\,\,\left( t\in \mathbb{R} \right)$ ta có: $f'\left( t \right)={{7}^{t}}\ln 7+6>0\,\,\left( \forall t\in \mathbb{R} \right)$ nên hàm số$f\left( t \right)$đồng biến trên $\mathbb{R}$ nên $f\left( x \right)=f\left( y \right)\Leftrightarrow x=y\Rightarrow x={{\log }_{7}}\left( 6x+1 \right)$

$\Leftrightarrow {{7}^{x}}=6x+1\Leftrightarrow g\left( x \right)={{7}^{x}}-6x-1=0$

Ta có: $g'\left( x \right)={{7}^{x}}\ln 7-6=0\Leftrightarrow x=\log \frac{6}{\ln 7}$

Suy ra BBT:

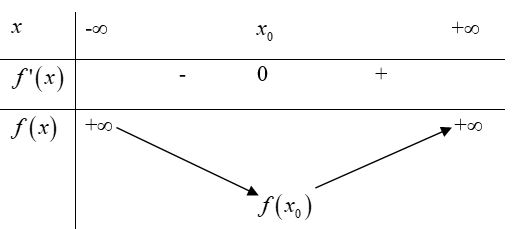
Do vậy PT $g\left( x \right)=0$ có nhiều nhất hai nghiệm. Mặt khác $g\left( 0 \right)=g\left( 1 \right)=0$

Vậy phương trình đã cho có hai nghiệm là $x=0;x=1.$

b) Điều kiện: $4-x>0$. Đặt $y={{\log }_{3}}\left( 4-x \right)\Rightarrow {{3}^{y}}=4-x$

Khi đó ${{3}^{x}}+4x=4-x+4{{\log }_{3}}\left( 4-x \right)={{3}^{y}}+4y\Rightarrow \left\{ \begin{array}  {} {{3}^{y}}=4-x \\  {} {{3}^{x}}=4-y \\ \end{array} \right.\Rightarrow x=y$

Đáp số: $x=1.$

Lời giải:

a) Ta có: ${{\log }_{3}}\frac{{{x}^{2}}+x+3}{2{{x}^{2}}+4x+5}=7\left( 2{{x}^{2}}+4x+5-{{x}^{2}}-x-3 \right)$.

$\Leftrightarrow {{\log }_{3}}\left( {{x}^{2}}+x+3 \right)+7\left( {{x}^{2}}+x+3 \right)={{\log }_{3}}\left( 2{{x}^{2}}+4x+5 \right)+7\left( 2{{x}^{2}}+4x+5 \right)$

Xét hàm số $f\left( t \right)={{\log }_{3}}t+t$ trên khoảng $\left( 0;+\infty  \right)$ ta có: $f'\left( t \right)=\frac{1}{t\ln 3}+1>0\,\,\,\,\forall t\in \left( 0;+\infty  \right)$

Do đó$f\left( {{x}^{2}}+x+3 \right)=f\left( 2{{x}^{2}}+4x+5 \right)\Leftrightarrow {{x}^{2}}+x+3=2{{x}^{2}}+4x+5\Leftrightarrow {{x}^{2}}+3x+2=0\Leftrightarrow \left[ \begin{array}  {} x=-1 \\  {} x=2 \\ \end{array} \right.$

Đáp số: $x=-1;x=-2.$

b) Điều kiện: $\left\{ \begin{array} {} x\ne 1 \\ {} 2x+1>0 \\ \end{array} \right.\Leftrightarrow \left\{ \begin{array}  {} x>-\frac{1}{2} \\  {} x\ne 1 \\ \end{array} \right.$.

Khi đó: $PT\Leftrightarrow 2{{x}^{2}}-6x+2={{\log }_{2}}\left( 2x+1 \right)-{{\log }_{2}}{{\left( x-1 \right)}^{2}}$

$\begin{array}  {} \Leftrightarrow 2\left( {{x}^{2}}-2x+1 \right)-2x={{\log }_{2}}\left( 2x+1 \right)-{{\log }_{2}}{{\left( x-1 \right)}^{2}} \\  {} \Leftrightarrow 2{{\left( x-1 \right)}^{2}}+{{\log }_{2}}{{\left( x-1 \right)}^{2}}=2x+1+{{\log }_{2}}\left( 2x+1 \right)-1 \\  {} \Leftrightarrow 2{{\left( x-1 \right)}^{2}}+{{\log }_{2}}{{\left( x-1 \right)}^{2}}=2\left( x+\frac{1}{2} \right)+{{\log }_{2}}\left( x+\frac{1}{2} \right) \\ \end{array}$

Xét hàm số $f\left( t \right)=2t+{{\log }_{2}}t\,\,\left( t\in \left( 0;+\infty  \right) \right)$ ta có $f'\left( t \right)=2+\frac{1}{t\ln 2}>0\,\,\,\forall t\in \left( 0;+\infty  \right)$

Do vậy $f\left[ {{\left( x-1 \right)}^{2}} \right]=f\left( x+\frac{1}{2} \right)\Leftrightarrow {{\left( x-1 \right)}^{2}}=x+\frac{1}{2}\Leftrightarrow x=\frac{3\pm \sqrt{7}}{2}\,\,\left( t/m \right).$

Lời giải:

Điều kiện: $x>\frac{-2}{3}$. Xét hàm số: $f\left( x \right)={{\log }_{2}}\left( 3x+2 \right)+{{\log }_{3}}\left( x+1 \right)$ với $x>-\frac{3}{2},f\left( 2 \right)=4$

Ta có: $f'\left( x \right)=\frac{3}{\left( 3x+2 \right)\ln 2}+\frac{1}{\left( x+1 \right)\ln 3}>0\,\,\,\,\forall x>\frac{-2}{3}\Rightarrow f\left( x \right)$ đồng biến $\forall x>\frac{-2}{3}$

Do vậy $f\left( x \right)=f\left( 2 \right)\Leftrightarrow x=2$

Vậy $x=2$là nghiệm duy nhất của PT đã cho. Chọn A.

Lời giải:

Điều kiện: $\frac{1}{2}<x\ne 1$. Khi đó $PT\Leftrightarrow {{\log }_{3}}\left( 2x-1 \right)-{{\log }_{3}}{{\left( x-1 \right)}^{2}}=3{{x}^{2}}-8x+5$

$\begin{array}  {} \Leftrightarrow {{\log }_{3}}\left( 2x-1 \right)={{\log }_{3}}\left( {{x}^{2}}-2x+1 \right)+1+\left( 3{{x}^{2}}-8x+4 \right) \\  {} \Leftrightarrow {{\log }_{3}}\left( 2x-1 \right)={{\log }_{3}}\left( 3{{x}^{2}}-6x+3 \right)+3{{x}^{2}}-6x+3-\left( 2x-1 \right) \\  {} \Leftrightarrow 2x-1+{{\log }_{3}}\left( 2x-1 \right)={{\log }_{3}}\left( 3{{x}^{2}}-6x+3 \right)+3{{x}^{2}}-6x+3 \\ \end{array}$

Xét hàm số $f\left( t \right)=t+{{\log }_{3}}t\,\,\left( t>0 \right)$ đồng biến trên khoảng $\left( 0;+\infty  \right)$

Do đó $f\left( 2x-1 \right)=f\left( 3{{x}^{2}}-6x+3 \right)\Leftrightarrow 2x-1=3{{x}^{2}}-6x+3\Leftrightarrow 3{{x}^{2}}-8x+4=0$

$\Leftrightarrow \left[ \begin{array}  {} x=2 \\  {} x=\frac{2}{3} \\ \end{array} \right.\Rightarrow $phương trình có hai nghiệm. Chọn B.

Lời giải:

Phương trình $\Leftrightarrow {{\log }_{2}}\left( {{x}^{2}}+x+2 \right)-{{\log }_{2}}\left( 2{{x}^{2}}-3x+5 \right)=\left( 2{{x}^{2}}-3x+5 \right)-\left( {{x}^{2}}+x+2 \right)$

$\Leftrightarrow {{\log }_{2}}\left( {{x}^{2}}+x+2 \right)+\left( {{x}^{2}}+x+2 \right)={{\log }_{2}}\left( 2{{x}^{2}}-3x+5 \right)+\left( 2{{x}^{2}}-3x+5 \right)$

Xét hàm số $f\left( t \right)={{\log }_{2}}t+t\,,\,\,t>0.$ Ta có: $f'\left( t \right)=\frac{1}{t\ln 2}+1>0\,\,\,\forall t>0\Rightarrow $Hàm $f$ đồng biến trên $\left( 0;+\infty  \right).$

Do đó: $f\left( {{x}^{2}}+x+2 \right)=f\left( 2{{x}^{2}}-3x+5 \right)\Leftrightarrow {{x}^{2}}+x+2=2{{x}^{2}}-3x+5\Leftrightarrow {{x}^{2}}-4x+3=0\Leftrightarrow \left[ \begin{array}  {} x=1 \\  {} x=3 \\ \end{array} \right..$

Vậy tập nghiệm của phương trình đã cho là: $\left\{ 1;3 \right\}$. Chọn D.