Con lắc đơn dao động trong điện trường là gì?

LÝ THUYẾT TRỌNG TÂM VÀ PHƯƠNG PHÁP GIẢI

Phương pháp chung:

Khi đặt con lắc vào điện trường đều có véc tơ cường độ điện trường $\overrightarrow{E}$ thì nó chịu tác dụng của trọng lực $\overrightarrow{P}$ và lực điện trường $\overrightarrow{F}=q\overrightarrow{E}$, hợp của hai lực này ký hiệu là $\overrightarrow{P'}=\overrightarrow{P}+\overrightarrow{F}$. (1).

P’ được gọi là trọng lực hiệu dụng hay trọng lực biểu kiến.

Chu kì dao động nhỏ của con lắc là $T'=2\pi \sqrt{\frac{\ell }{g'}}$.

Do đó để xác định được chu kì T’ ta cần xác định được gia tốc trọng trường hiệu dụng g’. Ta xét một số trường hợp thường gặp:

Trường hợp 1:

$\overrightarrow{E}$ có hướng thẳng đứng xuống dưới ( hay kí hiệu là $\overrightarrow{E}\downarrow $ )

Khi đó thì để xác định chiều của $\overrightarrow{F}$ ta cần biết dấu của q.

$\bullet $Nếu q<0, khi đó $\overrightarrow{F}\downarrow \uparrow \overrightarrow{E}$, ( hay $\overrightarrow{F}$ngược chiều với $\overrightarrow{E}$ ). Từ đó $\overrightarrow{F}$hướng thẳng đứng lên trên, từ (1) ta được: $P'=P-F\Leftrightarrow mg'=mg-\left| q \right|E\Leftrightarrow g'=g-\frac{\left| q \right|E}{m}$

$\to $ Chu kỳ dao động của con lắc khi đặt trong điện trường là: $T'=2\pi \sqrt{\frac{\ell }{g'}}=2\pi \sqrt{\frac{\ell }{g-\frac{\left| q \right|E}{m}}}$

$\bullet $Nếu q>0, khi đó $\overrightarrow{F}\uparrow \uparrow \overrightarrow{E}$, ( hay $\overrightarrow{F}$cùng chiều với $\overrightarrow{E}$ ). Từ đó $\overrightarrow{F}$hướng thẳng đứng xuống dưới, từ (1) ta được: $P'=P+F\Leftrightarrow mg'=mg+\left| q \right|E\Leftrightarrow g'=g+\frac{\left| q \right|E}{m}$

$\to $ Chu kỳ dao động của con lắc khi đặt trong điện trường là: $T'=2\pi \sqrt{\frac{\ell }{g'}}=2\pi \sqrt{\frac{\ell }{g+\frac{\left| q \right|E}{m}}}$

Trường hợp 2:

$\overrightarrow{E}$ có hướng thẳng đứng lên trên.

• Nếu q<0, khi đó $\overrightarrow{F}\downarrow \uparrow \overrightarrow{E}$ $\Rightarrow \overrightarrow{F}\downarrow $, từ (1) ta được : $P'=P+F\Leftrightarrow mg'=mg+\left| q \right|E\Leftrightarrow g'=g+\frac{\left| q \right|E}{m}$

$\to $Chu kỳ dao động của con lắc khi đặt trong điện trường là: $T'=2\pi \sqrt{\frac{\ell }{g'}}=2\pi \sqrt{\frac{\ell }{g+\frac{\left| q \right|E}{m}}}$

• Nếu q>0, khi đó $\overrightarrow{F}\uparrow \uparrow \overrightarrow{E}$$\Rightarrow \overrightarrow{F}\uparrow $, từ (1) ta được : $P'=P-F\Leftrightarrow mg'=mg-\left| q \right|E\Leftrightarrow g'=g-\frac{\left| q \right|E}{m}$

$\to $ Chu kỳ dao động của con lắc khi đặt trong điện trường là: $T'=2\pi \sqrt{\frac{\ell }{g'}}=2\pi \sqrt{\frac{\ell }{g-\frac{\left| q \right|E}{m}}}$

Nhận xét:

Tổng hợp cả hai trường hợp và các khả năng trong hai trường hợp trên ta thấy rằng khi véc tơ cường độ điện trường E có phương thẳng đứng (chưa xác định lên trên hay xuống dưới ) thì ta luôn có $g'=g\pm \frac{\left| q \right|E}{m}$. Từ đây, dựa vào gia tốc g’ lớn hơn hay nhỏ hơn g và dấu của điện tích q ta có thể xác định được ngay chiều của véc tơ cường độ điện trường.

Chúng ta có thể hiểu tổng quát như sau:

Nếu $\overrightarrow{E}$ hướng xuống ( cùng chiều với trọng lực ) ta có: $g'=g+\frac{\left| q \right|E}{m}$

Nếu $\overrightarrow{E}$hướng lên ( ngược chiều với trọng lực ) ta có: $g'=g-\frac{\left| q \right|E}{m}$

Trường hợp 3:

$\overrightarrow{E}$ có phương ngang, khi đó $\overrightarrow{F}$ cũng có phương ngang.

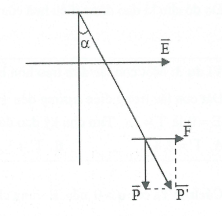
Do trọng lực P hướng xuống nên $\overrightarrow{F}\bot \overrightarrow{P}$.

Từ đó, $P{{'}^{2}}={{P}^{2}}+{{F}^{2}}\Leftrightarrow {{(mg')}^{2}}={{(mg)}^{2}}+{{(\left| q \right|E)}^{2}}$

$\Rightarrow g'=\sqrt{{{g}^{2}}+{{\left( \frac{\left| q \right|E}{m} \right)}^{2}}}\Rightarrow T'=2\pi \sqrt{\frac{\ell }{g'}}$

Góc lệch của con lắc so với phương ngang ( hay còn gọi là vị trí cân bằng của con lắc trong điện trường ) là $\alpha $ được cho bởi $\tan \alpha =\frac{F}{P}=\frac{\left| q \right|E}{mg}$