Biện luận số nghiệm của phương trình bằng đồ thị kết hợp với đặt ẩn phụ

Biện luận số nghiệm của phương trình bằng đồ thị kết hợp với đặt ẩn phụ
Bài toán: Cho hàm số $y=f\left( x \right)$. Biện luận số nghiệm của phương trình $f\left[ u\left( x \right) \right]=m$.
Phương pháp giải bài toán biện luận số nghiệm của phương trình
§ Bước 1: Đặt $t=u\left( x \right)$ ta cần xác định miền giá trị của $t$ và tương ứng với mỗi giá trị của $t$ có bao nhiêu giá trị của $x$.
(Ta có thể lập bảng biến thiên hàm số $t=u\left( x \right)$ để nhận xét và tìm miền của $t$).
§ Bước 2: Dựa vào đồ thị, biện luận số nghiệm của phương trình $f\left( t \right)=m$ từ đó suy ra số nghiệm của phương trình $f\left[ u\left( x \right) \right]=m$.
Bài tập vận dụng khó về biện luận số nghiệm của phương trình có đáp án
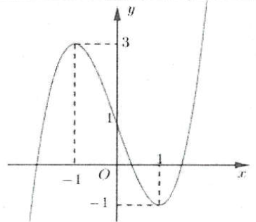
| Bài tập 1: [Đề thi tham khảo năm 2018] Cho hàm số $y=f\left( x \right)$ liên tục trên $\mathbb{R}$ và có đồ thị như hình vẽ bên
Tập hợp tất cả các giá trị thực của tham số $m$ để phương trình $f\left( \sin x \right)=m$ có nghiệm thuộc khoảng $\left( 0;\pi \right)$ là A. $\left[ -1;3 \right)$ B. $\left( -1;1 \right)$ C. $\left( -1;3 \right)$ D. $\left[ -1;1 \right)$ |
Lời giải chi tiết
Đặt $t=\sin x$, với $x\in \left( 0;\pi \right)\Rightarrow t\in \left( 0;1 \right]$. Khi đó $f\left( \sin x \right)=m\Leftrightarrow f\left( t \right)=m$.
Dựa vào đồ thị hàm số, để $f\left( t \right)=m$ có nghiệm thuộc $\left( 0;1 \right]$ $\Leftrightarrow -1\le m<1$. Chọn D.
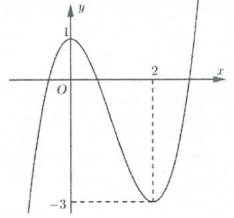
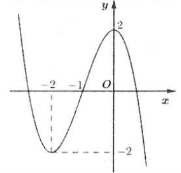
| Bài tập 2: Cho hàm số $y=f\left( x \right)={{x}^{3}}-3{{x}^{2}}+1$ liên tục trên $\mathbb{R}$và có đồ thị như hình vẽ bên.
Số các giá trị nguyên của tham số $m$ để phương trình $f\left( \sqrt{x}+\sqrt{1-x} \right)=m$ có nghiệm thuộc đoạn $\left[ 0;1 \right]$ là: A. 2 B. 3 C. 4 D. 5 |
Lời giải chi tiết
Đặt $t=\sqrt{x}+\sqrt{1-x}\Rightarrow {{t}^{2}}+2\sqrt{x\left( 1-x \right)}\left( t>0 \right)$
Theo bất đẳng thức Cosi ta có: $\sqrt{x\left( 1-x \right)}\le \frac{x+1-x}{2}=\frac{1}{2}$
Do đó $1\le {{t}^{2}}\le 2\Rightarrow 1\le t\le \sqrt{2}$. Vậy $x\in \left[ 0;1 \right]\Rightarrow t\in \left[ 1;\sqrt{2} \right]$
Ta có: $f\left( 1 \right)=-1,\,\,f\left( \sqrt{2} \right)=2\sqrt{2}-5$
Kết hợp đồ thị suy ra phương trình $f\left( t \right)=m$ có nghiệm thuộc đoạn $\left[ 1;\sqrt{2} \right]$ thì $m\in \left[ 2\sqrt{2}-5;-1 \right]$
Vậy có 2 giá trị nguyên của $m\in \left\{ -2;-1 \right\}$ để phương trình đã cho có nghiệm. Chọn A.
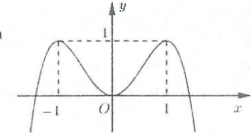
| Bài tập 3: Cho hàm số $y=f\left( x \right)=-{{x}^{4}}+2{{x}^{2}}$ liên tục trên $\mathbb{R}$ và có đồ thị như hình vẽ bên.
Số các giá trị nguyên của tham số $m$ để phương trình $-{{\left( 1-\sin x \right)}^{4}}+2{{\left( 1-\sin x \right)}^{2}}=m$ có nghiệm là: A. 2 B. 8 C. 3 D. 9 |
Lời giải chi tiết
Đặt $t=1-\sin x$ ta có: $\sin x\in \left[ -1;1 \right]\Rightarrow t\in \left[ 0;2 \right]$
Ta có: $f\left( 2 \right)=-8$. Dựa vào đồ thị hàm số ta thấy $t\in \left[ 0;2 \right]\Rightarrow f\left( t \right)\in \left[ -8;1 \right]$
Vậy phương trình $-{{\left( 1-\sin x \right)}^{4}}+2{{\left( 1-\sin x \right)}^{2}}=m$ có nghiệm khi $m\in \left[ -8;1 \right]$
Kết hợp $m\in \mathbb{Z}\Rightarrow $ có 9 giá trị của $m$. Chọn D.
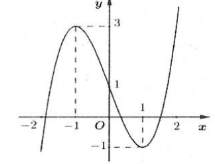
| Bài tập 4: Cho hàm số $y=f\left( x \right)$ có đồ thị như hình vẽ bên.
Số nghiệm của phương trình $f\left[ f\left( x \right) \right]=0$ là: A. 6 B. 7 C. 8 D. 9 |
Lời giải chi tiết
Đặt $t=f\left( x \right)\Rightarrow f\left( t \right)=0\Leftrightarrow \left[ \begin{array} {} t=f\left( x \right)=a \\ {} t=f\left( x \right)=b \\ {} t=f\left( x \right)=c \\ \end{array} \right.$ dựa vào đồ thị ta có: $a\in \left( -2;-1 \right),\,\,b\in \left( 0;1 \right),\,\,c\in \left( 1;2 \right)$
Khi đó dựa vào đồ thị ta lại có phương trình $f\left( x \right)=a$ có 1 nghiệm, phương trình $f\left( x \right)=b$ và phương trình $f\left( x \right)=c$ đều có 3 nghiệm.
Do đó phương trình $f\left[ f\left( x \right) \right]=0$ có 7 nghiệm. Chọn B.
| Bài tập 5: Cho hàm số $y=f\left( x \right)$ có đạo hàm trên $\mathbb{R}$ và có đồ thị là đường cong như hình vẽ.
Đặt $g\left( x \right)=f\left[ f\left( x \right) \right]$. Số nghiệm của phương trình ${g}'\left( x \right)=0$ là: A. 6 B. 7 C. 8 D. 9 |
Lời giải chi tiết
Ta có: ${g}'\left( x \right)={f}'\left( x \right).{f}'\left[ f\left( x \right) \right]=0\Leftrightarrow \left[ \begin{array} {} {f}'\left( x \right)=0 \\ {} {f}'\left[ f\left( x \right) \right]=0 \\ \end{array} \right.$
Dựa vào đồ thị hàm số ta thấy ${f}'\left( x \right)=0\Leftrightarrow \left[ \begin{array} {} x=-2 \\ {} x=0 \\ \end{array} \right.\Rightarrow {f}'\left( x \right)=0$ có 2 nghiệm phân biệt $x=-2,\,\,x=0$.
Lại có: ${f}'\left[ f\left( x \right) \right]=0\Leftrightarrow \left[ \begin{array} {} f\left( x \right)=-2 \\ {} f\left( x \right)=0 \\ \end{array} \right.$
Phương trình $f\left( x \right)=-2$ có 2 nghiệm $x=-2,\,\,x>0$ (nghiệm $x=-2$ bị lặp).
Phương trình $f\left( x \right)=0$ có 3 nghiệm phân biệt.
Do đó phương trình ${g}'\left( x \right)=0$ có 6 nghiệm phân biệt. Chọn A.
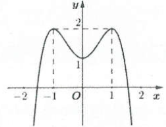
| Bài tập 6: Cho hàm số $y=f\left( x \right)=-{{x}^{4}}+2{{x}^{2}}+1$ có đồ thị như hình vẽ bên.
Số giá trị nguyên của $m$ để phương trình $f\left[ f\left( x \right) \right]=m$ có nghiệm $x\in \left[ -1;1 \right]$. A. 10 B. 11 C. 12 D. 13 |
Lời giải chi tiết
Dựa vào đồ thị hàm số ta thấy với $x\in \left[ -1;1 \right]\Rightarrow f\left( x \right)\in \left[ 1;2 \right]$
Đặt $t=f\left( x \right)$, xét phương trình $f\left( t \right)=m$ với $t\in \left[ 1;2 \right]$
Dựa vào đồ thị hàm số với $t\in \left[ 1;2 \right]\Rightarrow f\left( t \right)\in \left[ -7;2 \right]$
Do đó phương trình $f\left[ f\left( x \right) \right]=m$ có nghiệm $x\in \left[ -1;1 \right]\Leftrightarrow m\in \left[ -7;2 \right]$
Kết hợp $m\in \mathbb{Z}\Rightarrow $ có 10 giá trị của $m$. Chọn A.
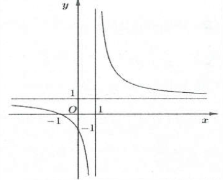
| Bài tập 7: Cho hàm số $y=\frac{x+1}{x-1}$ có đồ thị như hình vẽ.
Tìm $m$ để phương trình $\frac{\sin x+1}{\sin x-1}=m$ có nghiệm $x\in \left[ -\frac{\pi }{2};0 \right)$ A. $m\in \left[ -1;0 \right]$ B. $m\in \left[ -1;0 \right)$ C. $m\in \left[ -1;+\infty \right)$ D. $m\in \left( -1;0 \right]$ |
Lời giải chi tiết
Ta có: $x\in \left[ -\frac{\pi }{2};0 \right)\Rightarrow \sin x\in \left[ -1;0 \right)$. Đặt $t=\sin x\Rightarrow \frac{t+1}{t-1}=m$ với $t\in \left[ -1;0 \right)$
Dựa vào đồ thị hàm số ta thấy phương trình $f\left( t \right)=m$ có nghiệm $t\in \left[ -1;0 \right)\Leftrightarrow m\in \left( -1;0 \right]$. Chọn D.
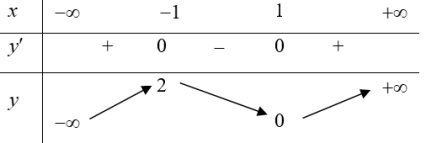
| Bài tập 8: Cho hàm số $y=f\left( x \right)$ có đạo hàm trên $\mathbb{R}$ và có bảng biến thiên như hình vẽ dưới đây
Số nghiệm của phương trình ${f}'\left[ f\left( x \right) \right]=0$ là: A. 4 B. 7 C. 6 D. 3 |
Lời giải chi tiết
Đặt $g\left( x \right)=f\left[ f\left( x \right) \right]$ ta có: ${g}'\left( x \right)={f}'\left( x \right).{f}'\left[ f\left( x \right) \right]=0\Leftrightarrow \left[ \begin{array} {} {f}'\left( x \right)=0 \\ {} {f}'\left[ f\left( x \right) \right]=0 \\ \end{array} \right.$
Dựa vào đồ thị hàm số ta thấy ${f}'\left( x \right)=0\Leftrightarrow \left[ \begin{array} {} x=-1 \\ {} x=1 \\ \end{array} \right.\Rightarrow {f}'\left( x \right)=0$ có 2 nghiệm phân biệt $x=\pm 1$.
Lại có: ${f}'\left[ f\left( x \right) \right]=0\Leftrightarrow \left[ \begin{array} {} f\left( x \right)=-1 \\ {} f\left( x \right)=1 \\ \end{array} \right.$Phương trình $f\left( x \right)=-1$ có một nghiệm duy nhất
Phương trình $f\left( x \right)=1$ có 3 nghiệm phân biệt.
Do đó phương trình ${g}'\left( x \right)=0$ có 6 nghiệm phân biệt. Chọn C.
TOÁN LỚP 12