Bài toán mặt cầu của một số tứ diện đặc biệt

Bài toán mặt cầu của một số tứ diện đặc biệt

Các bài toán mặt cầu mẫu

R Mẫu 1: Cho tứ diện ABCD có $AB=CD=a,AC=BD=b,AD=BC=c$ (tứ diện gần đều)

Bán kính mặt cầu ngoại tiếp tứ diện là: $R=\sqrt{\frac{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}{8}}.$

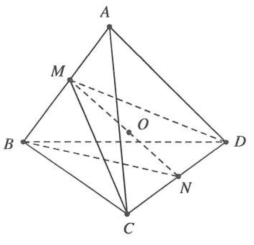
Chứng minh: Gọi $M,N,O$ lần lượt là trung điểm của $AB;CD$ và $MN$

Ta có: $\Delta ACD=\Delta BDC\left( c-c-c \right)\Rightarrow DM=CM$

Khi đó $MN\bot CD,$ tương tự $MN\bot AB$ suy ra O là tâm mặt cầu ngoại tiếp tứ diện.

Ta có: ${{R}^{2}}=O{{A}^{2}}=O{{B}^{2}}=O{{M}^{2}}+A{{M}^{2}}=\frac{M{{N}^{2}}}{4}+\frac{{{a}^{2}}}{4}$

Xét $\Delta CMN$ có: $M{{N}^{2}}=C{{M}^{2}}-C{{N}^{2}}=\frac{{{b}^{2}}+{{c}^{2}}}{2}-\frac{{{a}^{2}}}{4}-\frac{{{a}^{2}}}{4}$

$=\frac{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}}{2}\Rightarrow {{R}^{2}}=\frac{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}}{8}+\frac{{{a}^{2}}}{4}=\frac{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}{8}.$

Vậy$R=\sqrt{\frac{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}{8}}.$

Bài tập bài toán mặt cầu của một số tứ diện đặc biệt

Lời giải chi tiết

Áp dụng công thức nhanh ta có: $R=\sqrt{\frac{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}{8}}=\sqrt{\frac{{{3}^{2}}+{{2}^{2}}+{{\left( 2\sqrt{2} \right)}^{2}}}{8}}=\sqrt{\frac{21}{8}}\Rightarrow S=4\pi {{R}^{2}}=\frac{21\pi }{2}.$

Chọn A.

Lời giải chi tiết

Áp dụng công thức nhanh ta có: $R=\sqrt{\frac{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}{8}}=R=\sqrt{\frac{{{a}^{2}}+2{{b}^{2}}}{8}}.$ Chọn A.

Lời giải chi tiết

Áp dụng công thức nhanh ta có: $R=\sqrt{\frac{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}{8}}=\sqrt{\frac{{{1}^{2}}+{{2}^{2}}+{{2}^{2}}}{8}}=\frac{3}{2\sqrt{2}}\Rightarrow V=\frac{4}{3}\pi {{R}^{3}}=\frac{9\pi \sqrt{2}}{8}.$

Chọn D.

Lời giải chi tiết

Bán kính mặt cầu ngoại tiếp tứ diện ABCD là $R=\sqrt{\frac{A{{B}^{2}}+A{{C}^{2}}+A{{D}^{2}}}{8}}=\frac{\sqrt{35}}{2}.$

Vậy thể tích khối cầu ngoại tiếp tứ diện ABCD là $V=\frac{4}{3}\pi {{R}^{3}}=\frac{4}{3}\pi .{{\left( \frac{\sqrt{35}}{2} \right)}^{3}}=\frac{35\sqrt{35}\pi }{6}.$ Chọn C.

Lời giải chi tiết

Bán kính mặt cầu ngoại tiếp tứ diện ABCD là $R=\sqrt{\frac{A{{B}^{2}}+A{{C}^{2}}+A{{D}^{2}}}{8}}.$

Khi đó $\sqrt{\frac{{{x}^{2}}+{{y}^{2}}+{{\left( 2\sqrt{3} \right)}^{2}}}{8}}=\sqrt{2}\Leftrightarrow {{x}^{2}}+{{y}^{2}}=4$ mà $xy\le \frac{{{x}^{2}}+{{y}^{2}}}{2}=\frac{4}{2}=2.$

Dấu bằng xảy ra khi và chỉ khi $x=y=\sqrt{2}.$ Vậy ${{\left\{ xy \right\}}_{\max }}=2.$ Chọn A.

R Mẫu 2: Cho tứ diện ABCD có $AB=x;CD=y;AD=BC=AC=BD=z.$ Tính bán kính mặt cầu ngoại tiếp tứ diện ABCD. 

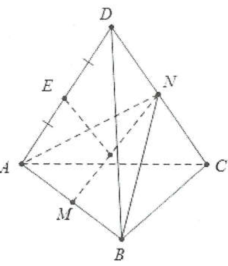
Gọi $M,N$ lần lượt là trung điểm của AB và CD ta có:

$\Delta DAC=\Delta DBC\Rightarrow AN=BN$ suy ra $NM$ là trung trực của AB, tương tự MN là trung trực của DC

Khi đó $I\in MN$ sao cho $ID=IA$

Lại có $AN=\sqrt{A{{D}^{2}}-D{{N}^{2}}}=\sqrt{{{z}^{2}}-\frac{{{y}^{2}}}{4}}$

$\Rightarrow MN=\sqrt{A{{N}^{2}}-A{{M}^{2}}}=\sqrt{{{z}^{2}}-\frac{{{y}^{2}}}{4}-\frac{{{x}^{2}}}{4}}$

Mặt khác $MN=IM+IN=\sqrt{{{R}^{2}}-A{{M}^{2}}}+\sqrt{{{R}^{2}}-D{{N}^{2}}}$

$\Rightarrow \sqrt{{{R}^{2}}-\frac{{{x}^{2}}}{4}}+\sqrt{{{R}^{2}}-\frac{{{y}^{2}}}{4}}=\sqrt{{{z}^{2}}-\frac{{{y}^{2}}}{4}-\frac{{{z}^{2}}}{4}}$

Vậy bán kính mặt cầu ngoại tiếp tứ diện ABCD là nghiệm của phương trình:

$\sqrt{{{R}^{2}}-\frac{{{x}^{2}}}{4}}+\sqrt{{{R}^{2}}-\frac{{{y}^{2}}}{4}}=\sqrt{{{z}^{2}}-\frac{{{y}^{2}}}{4}-\frac{{{z}^{2}}}{4}}.$

Lời giải chi tiết

Ta có: $\sqrt{{{R}^{2}}-{{a}^{2}}}+\sqrt{{{R}^{2}}-4{{a}^{2}}}=\sqrt{9{{a}^{2}}-5{{a}^{2}}}=2a$

$\Leftrightarrow \sqrt{{{R}^{2}}-{{a}^{2}}}=\left( 2a-\sqrt{{{R}^{2}}-4{{a}^{2}}} \right)\Rightarrow {{R}^{2}}-{{a}^{2}}=4{{a}^{2}}-4a\sqrt{{{R}^{2}}-4{{a}^{2}}}+{{R}^{2}}-4{{a}^{2}}$

Chọn B.

Lời giải chi tiết

Ta có: $\sqrt{{{R}^{2}}-4{{a}^{2}}}+\sqrt{{{R}^{2}}-9{{a}^{2}}}=\sqrt{22{{a}^{2}}-13{{a}^{2}}}=3a$

$\Leftrightarrow \sqrt{{{R}^{2}}-4{{a}^{2}}}=\left( 3a-\sqrt{{{R}^{2}}-9{{a}^{2}}} \right)\Rightarrow {{R}^{2}}-4{{a}^{2}}=9{{a}^{2}}-6a\sqrt{{{R}^{2}}-9{{a}^{2}}}+{{R}^{2}}-9{{a}^{2}}$

$\Leftrightarrow \sqrt{{{R}^{2}}-9{{a}^{2}}}=\frac{4a}{6}\Leftrightarrow R=\frac{a\sqrt{85}}{4}\Rightarrow S=4\pi {{R}^{2}}=\frac{340\pi }{9}.$ Chọn C.

Lời giải chi tiết

Ta có: $\sqrt{{{R}^{2}}-{{a}^{2}}}+\sqrt{{{R}^{2}}-9{{a}^{2}}}=\sqrt{26{{a}^{2}}-10{{a}^{2}}}=4a$

$\Leftrightarrow \sqrt{{{R}^{2}}-{{a}^{2}}}=\left( 4a-\sqrt{{{R}^{2}}-9{{a}^{2}}} \right)\Rightarrow {{R}^{2}}-{{a}^{2}}=16{{a}^{2}}-8a\sqrt{{{R}^{2}}-9{{a}^{2}}}+{{R}^{2}}-9{{a}^{2}}$

$\Leftrightarrow \sqrt{{{R}^{2}}-9{{a}^{2}}}=a\Leftrightarrow R=a\sqrt{10}.$ Chọn C.

Lời giải chi tiết

Ta có: $\sqrt{{{R}^{2}}-4{{a}^{2}}}+\sqrt{{{R}^{2}}-25{{a}^{2}}}=\sqrt{78{{a}^{2}}-29{{a}^{2}}}=7a$

$\Leftrightarrow \sqrt{{{R}^{2}}-4{{a}^{2}}}=\left( 7a-\sqrt{{{R}^{2}}-25{{a}^{2}}} \right)\Rightarrow {{R}^{2}}-4{{a}^{2}}=49{{a}^{2}}-14a\sqrt{{{R}^{2}}-25{{a}^{2}}}+{{R}^{2}}-25{{a}^{2}}$

$\Leftrightarrow \sqrt{{{R}^{2}}-25{{a}^{2}}}=2a\Leftrightarrow R=a\sqrt{29}\Rightarrow {{S}_{\left( C \right)}}=4\pi {{R}^{2}}=116\pi {{a}^{2}}.$ Chọn D.

Lời giải chi tiết

Ta có: $\sqrt{{{R}^{2}}-{{a}^{2}}}+\sqrt{{{R}^{2}}-16{{a}^{2}}}=\sqrt{{{x}^{2}}-17{{a}^{2}}}$

Với$R=a\sqrt{17}\Rightarrow \sqrt{{{x}^{2}}-17{{a}^{2}}}=4a+a=5a\Rightarrow {{x}^{2}}=42{{a}^{2}}\Rightarrow x=a\sqrt{42}.$ Chọn A...