Bài toán Đa diện có các đỉnh cùng nhìn một đoạn nối hai đỉnh còn lại dưới góc vuông

Bài toán Đa diện có các đỉnh cùng nhìn một đoạn nối hai đỉnh còn lại dưới góc vuông

Phương pháp giải:

Xét đa giác $XY{{A}_{1}}{{A}_{2}}...{{A}_{n}}$ có các đỉnh ${{A}_{1}},{{A}_{2}},...,{{A}_{n}}$cùng nhìn XY một góc vuông, chẳng hạn có $\widehat{{{A}_{1}}XY}=\widehat{{{A}_{2}}XY}=...=90_{{}}^{0}.$ Khi đó, mặt cầu ngoại tiếp đa diện $XY{{A}_{1}}{{A}_{2}}...{{A}_{n}}$ mặt cầu đường kính XY, tâm là trung điểm của XY và bán kính $R=\frac{XY}{2}.$

Bài tập có đáp án chi tiết

Lời giải chi tiết

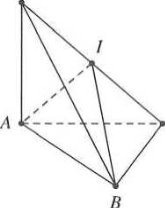
Vì $SA\bot \left( ABC \right)$ nên $\left( \widehat{SB;(ABC)} \right)=\left( \widehat{AB;AB} \right)=\widehat{SBA}={{45}^{0}}.$

Suy ra tam giác SAB vuông cân tại $A\xrightarrow{{}}SA=AB=a.$

Ta có $A{{B}^{2}}+B{{C}^{2}}={{a}^{2}}+{{\left( a\sqrt{3} \right)}^{2}}=4{{a}^{2}}=A{{C}^{2}}\Rightarrow \Delta ABC$ vuông tại B.

Do đó $AB\bot BC$ mà $BC\bot SA\Leftrightarrow BC\bot \left( SAB \right)\Rightarrow BC\bot SB$

Khi đó, hai điểm A, B cùng nhìn SC dưới một góc vuông

Vậy bán kính mặt cầu ngoại tiếp cần tính là $R=\frac{SC}{2}=\frac{a\sqrt{5}}{2}.$

Chọn A.

Lời giải chi tiết

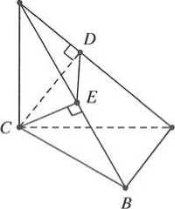
Ta có $\left\{ \begin{matrix}   SC\bot AB  \\   BC\bot AB  \\\end{matrix} \right.\Rightarrow AB\left( SBC \right)\Rightarrow CE\bot AB$

Mà $SA\bot \left( \alpha  \right)\Rightarrow SA\bot CE$suy ra $CE\bot \left( SAB \right)\Rightarrow \left\{ \begin{matrix}   CE\bot SB  \\   CE\bot AE  \\\end{matrix} \right.,$

Do đó các điểm $B,D,E$ nhìn AC dưới một góc vuông

$\Rightarrow$ Tâm mặt cầu ngoại tiếp khối đa diện là trung điểm AC

$\Rightarrow R=\frac{AC}{2}=\frac{AB\sqrt{2}}{2}=a\xrightarrow{{}}S=4\pi {{a}^{2}}.$ Chọn B.

Lời giải chi tiết

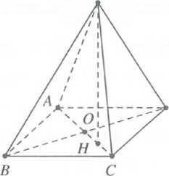
Gọi H là trung điểm của $OC\Rightarrow SH\bot \left( ABCD \right),HC=\frac{OC}{2}=\frac{a}{4}$

Ta có $\widehat{SC;\left( ABCD \right)}=\left( \widehat{SC;HC} \right)=\widehat{SCH}={{60}^{0}}$

Tam giác SHC vuông tại H, có $\cos \widehat{SCH}=\frac{HC}{SC}\Rightarrow SC=\frac{a}{2}$

Lại có $SH\bot OC\Rightarrow \Delta SOC$ cân tại $S\Rightarrow SO=SC=\frac{a}{2}$ 

Do đó $SO=OA=OC$ mà $OA=OB=OC=OD$

Suy ra O là tâm mặt cầu ngoại tiếp hình chóp $S.ABCD$

Vậy $R=\frac{BD}{2}=\frac{a}{2}\xrightarrow{{}}V=\frac{4}{3}\pi {{R}^{3}}=\frac{\pi {{a}^{3}}}{6}.$ Chọn D.

Lời giải chi tiết

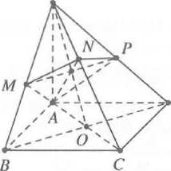
Ta có $SC\bot \left( AMNP \right)\Rightarrow SC\bot AM$ mà $AM\bot SB$

$\Rightarrow AM\bot MC\Rightarrow \widehat{AMC}={{90}^{0}}.$ Tương tự $\widehat{APC}={{90}^{0}}$

Mặt khác $\widehat{ANC}={{90}^{0}}$ nên tâm mặt cầu ngoại tiếp tứ diện $C.MNP$ là trung điểm của AC

Suy ra $R=\frac{AC}{2}=2\Rightarrow V=\frac{4}{3}\pi {{R}^{3}}=\frac{32}{3}\pi .$ Chọn C.

Lời giải chi tiết

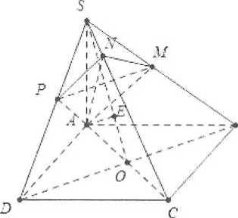
Ta có: $\left\{ \begin{matrix}   BC\bot AB  \\   BC\bot SA  \\\end{matrix}\Rightarrow BC\bot AM \right.$

Mặt khác: $AM\bot SC\Rightarrow AM\bot \left( SBC \right)\Rightarrow AM\bot MN$

Tương tự $AP\bot PN\Rightarrow$ tứ giác $AMNP$ nội tiếp đường tròn đường kính $AN\Rightarrow {{R}_{MNP}}={{R}_{AMNP}}=\frac{AN}{2}$

Gọi O là tâm hình vuông ABCD, dựng $AE\bot SO\Rightarrow AE=\frac{6}{\sqrt{13}}$

Do đó $AO=\frac{AC}{2}=2\Rightarrow \frac{1}{A{{E}^{2}}}=\frac{1}{S{{A}^{2}}}+\frac{1}{A{{O}^{2}}}\Rightarrow SA=3$

$\Rightarrow AN=\frac{SA.AC}{\sqrt{S{{A}^{2}}+A{{C}^{2}}}}=\frac{12}{5}\Rightarrow {{R}_{MPN}}=\frac{6}{5};SN=\frac{S{{A}^{2}}}{SC}=\frac{9}{5}\Rightarrow {{R}_{S.MPN}}=\sqrt{R_{MNP}^{2}+\frac{S{{N}^{2}}}{4}}=\frac{3}{2}$

$\Rightarrow {{V}_{S.MPN}}=\frac{4}{3}\pi {{R}^{3}}=\frac{9\pi }{2}.$ Chọn C.