Diện tích hình phẳng giới hạn bởi các đồ thị \(y={{x}^{2}}\) và \(y=\left| x-2 \right|\) bằng
Phương pháp giải
Tìm hoành độ giao điểm của 2 đồ thị hàm số, áp dụng công thức tính diện tích hình phẳng và tích phân hàm trị tuyệt đối.
Công thức tính diện tích hình phẳng được giới hạn bởi các đồ thị hàm số \(y=f\left( x \right);\ \ y=g\left( x \right)\) và các đường thẳng \(x=a;\ \ x=b\ \left( a<b \right)\) là : \(S=\int\limits_{a}^{b}{\left| f\left( x \right)-g\left( x \right) \right|dx.}\)
Lời giải của Tự Học 365
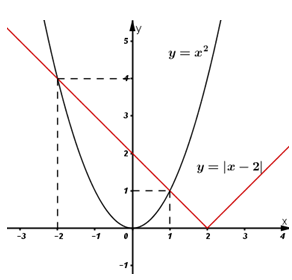
Hoành độ giao điểm của \(\left( C \right)\) và \(\left( d \right)\) là nghiệm phương trình: \({{x}^{2}}=\left| x-2 \right|\)
\(\begin{array}{l}
\Leftrightarrow {x^4} = {x^2} - 4x + 4 \Leftrightarrow {x^4} - {x^2} + 4x - 4 = 0\\
\Leftrightarrow \left( {x - 1} \right)\left( {{x^3} + {x^2} + 4} \right) = 0\\
\Leftrightarrow \left( {x - 1} \right)\left( {x + 2} \right)\left( {{x^2} - x + 2} \right) = 0\\
\Leftrightarrow \left[ \begin{array}{l}
x - 1 = 0\\
x + 2 = 0\\
{x^2} - x + 2 = 0
\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}
x = - \,2\\
x = 1
\end{array} \right..
\end{array}\)
Diện tích hình phẳng cần tính là :
\(\begin{align} & S=\int\limits_{-\,2}^{1}{\left| {{x}^{2}}-\left| x-2 \right| \right|\,\text{d}x}=\int\limits_{-\,2}^{1}{\left| {{x}^{2}}-\left( -x+2 \right) \right|\,\text{d}x}=\int\limits_{-\,2}^{1}{\left| {{x}^{2}}+x-2 \right|\,\text{d}x} \\& =\int\limits_{-\,2}^{1}{\left( -{{x}^{2}}-x+2 \right)\,\text{d}x}=\left. \left( -\frac{{{x}^{3}}}{3}-\frac{{{x}^{2}}}{2}+2x \right) \right|_{-2}^{1}=\frac{9}{2}. \\\end{align}\)
Đáp án cần chọn là: c
Toán Lớp 12
