Câu hỏi
Vận dụng
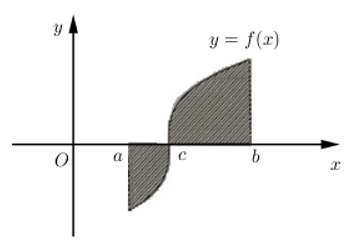
Cho hàm số \(y=f\left( x \right)\) liên tục trên đoạn \(\left[ a;b \right]\) và cắt trục hoành tại điểm \(x=c\,\,\left( a<c<b \right)\) (như hình vẽ bên) Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y=f\left( x \right)\), trục hoành và hai đường thẳng \(x=a;x=b\). Mệnh đề nào dưới đây đúng ?
Đáp án đúng: b
Phương pháp giải
Ứng dụng tích phân để tính diện tích hình phẳng.
Lời giải của Tự Học 365
\(S=\int\limits_{a}^{b}{\left| f\left( x \right) \right|dx}=\int\limits_{a}^{c}{\left| f\left( x \right) \right|dx}+\int\limits_{c}^{b}{\left| f\left( x \right) \right|dx}=-\int\limits_{a}^{c}{f\left( x \right)dx}+\int\limits_{c}^{b}{f\left( x \right)dx}\)
Đáp án cần chọn là: b
Toán Lớp 12
