Cho hình chóp đều \(S.ABCD\)có tất cả các cạnh bằng \(a\), điểm \(M\) thuộc cạnh \(SC\) sao cho \(SM = 2MC\). Mặt phẳng \(\left( P \right)\) chứa \(AM\) và song song với \(BD\). Tính diện tích thiết diện của hình chóp \(S.ABCD\) cắt bởi \(\left( P \right)\).
Phương pháp giải
- Xác định thiết diện và nhận dạng thiết diện, từ đó tính diện tích.
Lời giải của Tự Học 365
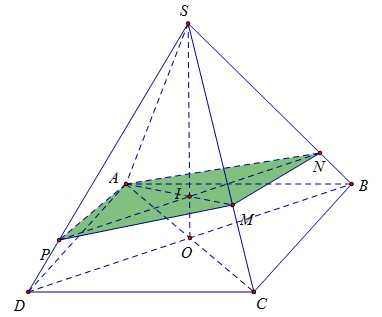
Gọi \(O = AC \cap BD\), \(I = AM \cap SO\).
Trong \(\left( {SBD} \right)\) từ \(I\) kẻ đường thẳng \(\Delta \) song song với \(BD\) cắt \(SB\), \(SD\) lần lượt tại \(N\), \(P\).
Suy ra thiết diện là tứ giác \(ANMP\).
Ta có: \(\left\{ \begin{array}{l}BD \bot AC\\BD \bot SO\end{array} \right.\)\( \Rightarrow BD \bot \left( {SAC} \right)\)
\( \Rightarrow BD \bot AM\).
Mặt khác: \(BD//NP\).
\( \Rightarrow AM \bot NP\).
\( \Rightarrow {S_{ANMP}} = \dfrac{1}{2}NP.AM\).
+ Tính \(AM\):
Ta có: \(\left\{ \begin{array}{l}SA = SC = a\\AC = a\sqrt 2 \end{array} \right.\)\( \Rightarrow \Delta SAC\) vuông cân tại \(S\).
\( \Rightarrow AM = \sqrt {S{A^2} + S{M^2}} \)\( = \sqrt {{a^2} + {{\left( {\dfrac{2}{3}a} \right)}^2}} \)\( = \dfrac{{a\sqrt {13} }}{3}\).
+ Tính \(AM\):
Ta có: \(NP//BD\)\( \Rightarrow \dfrac{{NP}}{{BD}} = \dfrac{{SI}}{{SO}}\)\( \Rightarrow NP = \dfrac{{SI.BD}}{{SO}}\).
Tính \(\dfrac{{SI}}{{SO}}\):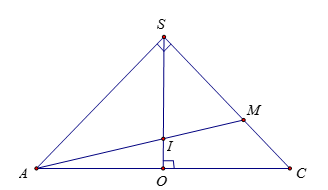
Gọi \(\dfrac{{SI}}{{SO}} = k\).
Ta có: \(\overrightarrow {AI} = \overrightarrow {AS} + \overrightarrow {SI} \)\( = - \overrightarrow {SA} + k\overrightarrow {SO} \).
\(\overrightarrow {AM} = \overrightarrow {AS} + \overrightarrow {SM} \)\( = - \overrightarrow {SA} + \dfrac{2}{3}\overrightarrow {SC} \).
\(A\), \(I\), \(M\) thẳng hàng \( \Leftrightarrow \) \(\overrightarrow {AI} = l\overrightarrow {AM} \)\( \Leftrightarrow - \overrightarrow {SA} + k\overrightarrow {SO} = - \overrightarrow {lSA} + \dfrac{2}{3}l\overrightarrow {SC} \)
\( \Leftrightarrow - \overrightarrow {SA} + \dfrac{k}{2}\left( {\overrightarrow {SA} + \overrightarrow {SC} } \right) = - \overrightarrow {lSA} + \dfrac{2}{3}l\overrightarrow {SC} \)\( \Leftrightarrow \left\{ \begin{array}{l}\dfrac{1}{2}k + l = 1\\\dfrac{1}{2}k - \dfrac{2}{3}l = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}k = \dfrac{4}{5}\\l = \dfrac{3}{5}\end{array} \right.\) .
\( \Rightarrow \dfrac{{SI}}{{SO}} = \dfrac{4}{5}\)\( \Rightarrow NP = \dfrac{4}{5}BD\)\( = \dfrac{{4a\sqrt 2 }}{5}\).
\( \Rightarrow {S_{ANMP}} = \dfrac{1}{2}NP.AM\)\( = \dfrac{1}{2}.\dfrac{{4a\sqrt 2 }}{5}.\dfrac{{a\sqrt {13} }}{3}\)\( = \dfrac{{2\sqrt {26} {a^2}}}{{15}}\).
Đáp án cần chọn là: c
Toán Lớp 12
