Lời giải của Tự Học 365

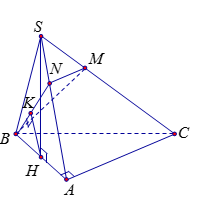
Cách 1. Gọi \(H\) là trung điểm của \(AB\) suy ra \(SH \bot \left( {ABC} \right).\)

Trong $\left( {SAC} \right)$ từ \(M\) dựng \(MN\;{\rm{//}}\;AC\), gọi \(K\) là hình chiếu của \(H\) trên \(BN.\)

Ta có \(AC \bot \left( {SAB} \right)\) mà \(MN\;{\rm{//}}\;AC \Rightarrow MN \bot \left( {SAB} \right)\)

\(\left\{ {\begin{array}{*{20}{c}}{HK \bot BN}\\{HK \bot MN}\end{array}} \right. \Rightarrow HK \bot \left( {BMN} \right).\)

 Vì \(\left( {BMN} \right)\;{\rm{//}}\;AC\) suy ra khoảng cách giữa hai đường \(AC\) và \(BM\) là

$d\left( {A,\left( {BMN} \right)} \right) = 2d\left( {H,\left( {BMN} \right)} \right) = 2HK = 2BH\sin \widehat {ABN}$

Trong tam giác \(SAB\) hạ \(NF \bot AB\), suy ra \(NF = \dfrac{2}{3}SH = \dfrac{2}{3}.\dfrac{{4\sqrt 3 }}{2} = \dfrac{{4\sqrt 3 }}{3}\), và

\(BF = BH + HF = BH + \dfrac{1}{3}AH = 2 + \dfrac{2}{3} = \dfrac{8}{3}\).  

Vậy $BN = \sqrt {B{F^2} + N{F^2}}  = \dfrac{{a\sqrt 7 }}{3}$, $\dfrac{{BN}}{{\sin 60^\circ }} = \dfrac{{AN}}{{\sin \widehat {ABN}}}$$ \Leftrightarrow \sin \widehat {ABN} = \dfrac{{\dfrac{{2a}}{3}.\dfrac{{\sqrt 3 }}{2}}}{{\dfrac{{a\sqrt 7 }}{3}}} = \dfrac{{\sqrt 3 }}{{\sqrt 7 }}.$

Suy ra $d\left( {A,\left( {BMN} \right)} \right) = 2.2.\dfrac{{\sqrt 3 }}{{\sqrt 7 }} = \dfrac{{4\sqrt {21} }}{7}.$

Đáp án cần chọn là: a