Lời giải của Tự Học 365

Xét hình lăng trụ tam giác đều có các cạnh đều bằng \(2\).

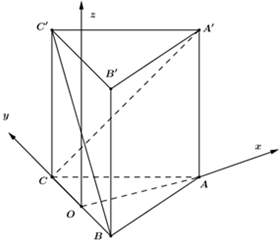
Chọn hệ trục tọa độ như hình vẽ có gốc tọa độ là trung điểm của \(BC.\) 

Ta có các điểm: \(O\left( {0;\;0;\;0} \right);\;A \in Ox \Rightarrow A\left( {\sqrt 3 ;\;0;\;0} \right)\)

\(\begin{array}{l}B;\;C \in Oy \Rightarrow B\left( {0;\; - 1;\;0} \right),\;\;C\left( {0;\;1;\;0} \right).\\A'\left( {\sqrt 3 ;\;0;\;2} \right);\;C'\left( {0;\;1;\;2} \right).\\ \Rightarrow \overrightarrow {A'C}  = \left( { - \sqrt 3 ;\;1;\; - 2} \right);\;\;\overrightarrow {BC}  = \left( {0;\;2;\;2} \right) = \left( {0;\;1;\;1} \right).\end{array}\)

Phương trình đường thẳng \(A'C\) là: \(\left\{ \begin{array}{l}x =  - \sqrt 3 {t_1}\\y = 1 + {t_1}\\z =  - 2{t_1}\end{array} \right..\)

Phương trình đường thẳng \(BC'\) là: \(\left\{ \begin{array}{l}x = 0\\y =  - 1 + {t_2}\\z = {t_2}\end{array} \right..\)

Ta có điểm \(M \in A'C \Rightarrow M\left( { - \sqrt 3 {t_1};1 + {t_1}; - 2{t_1}} \right);\;N \in BC' \Rightarrow N\left( {0;\; - 1 + {t_2};\;{t_2}} \right).\)

\( \Rightarrow \overrightarrow {MN} \left( {\sqrt 3 {t_1};\;{t_2} - {t_1} - 2;\;{t_2} + 2{t_1}} \right)\)

\(MN\) là đoạn vuông góc chung của \(A'C\) và \(BC' \Rightarrow \left\{ \begin{array}{l}MN \bot A'C\\MN \bot BC'\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\overrightarrow {MN} .\overrightarrow {AC'}  = 0\\\overrightarrow {MN} .\overrightarrow {BC'}  = 0\end{array} \right.\)

\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l} - \sqrt 3 {t_1}.\sqrt 3  + {t_2} - {t_1} - 2 - 2\left( {{t_2} + 2{t_1}} \right) = 0\\{t_2} - {t_1} - 2 + {t_2} + 2{t_1} = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 8{t_1} - {t_2} = 2\\{t_1} + 2{t_2} = 2\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{t_1} =  - \dfrac{2}{5}\\{t_2} = \dfrac{6}{5}\end{array} \right. \Rightarrow N\left( {0;\;\dfrac{1}{5};\;\dfrac{6}{5}} \right) \Rightarrow \left\{ \begin{array}{l}\overrightarrow {NB}  = \left( {0;\; - \dfrac{6}{5};\; - \dfrac{6}{5}} \right)\\\overrightarrow {NC'}  = \left( {0;\;\dfrac{4}{5};\;\dfrac{4}{5}\;} \right)\end{array} \right..\\ \Rightarrow \dfrac{{NB}}{{NC}} = \dfrac{{\left| {\overrightarrow {NB} } \right|}}{{\left| {\overrightarrow {NC'} } \right|}} = \dfrac{{\sqrt {\dfrac{{36}}{{25}}.2} }}{{\sqrt {\dfrac{{16}}{{25}}.2} }} = \sqrt {\dfrac{9}{4}}  = \dfrac{3}{2}.\end{array}\)

Đáp án cần chọn là: a